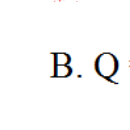Học tại trường
Chưa có thông tin
Đến từ
Ninh Bình , Chưa có thông tin
Số lượng câu hỏi
5
Số lượng câu trả lời
64
Điểm GP
15
Điểm SP
59
Người theo dõi (8)
Đang theo dõi (15)

Câu trả lời:
cậu vào câu hỏi tương tự

Câu trả lời:
tan36=cot54 => tan36-cot54=cot54-cot54=0


Câu trả lời:
101 + 2 + 3
vậy số lớn nhất là 101