Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
0
Số lượng câu trả lời
120
Điểm GP
69
Điểm SP
154










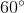 . Goc này chắn cung
. Goc này chắn cung 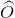 =
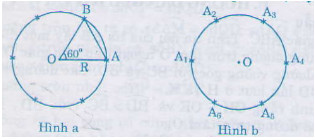
= 
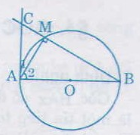
 :
: 
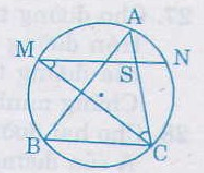
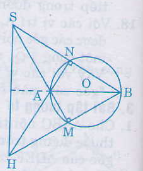
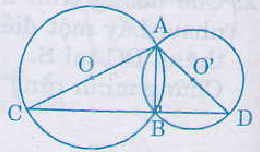

 =
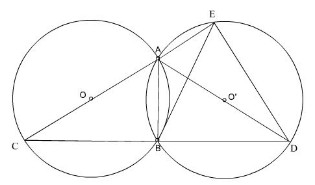
= 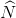 (cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B 
