
Gọi MN = 2R là đường kính của đường tròn có cung tròn là ![]()
Theo bài tập 23, ta có:
KA. KB = KM. KN
hay KA. KB = KM. (2R - KM)
Thay số, ta có:
20. 20 = 3(2R - 3)
do đó 6R = 400 + 9 = 4099.
Vậy R = ≈688,2(mét)

Gọi MN = 2R là đường kính của đường tròn có cung tròn là ![]()
Theo bài tập 23, ta có:
KA. KB = KM. KN
hay KA. KB = KM. (2R - KM)
Thay số, ta có:
20. 20 = 3(2R - 3)
do đó 6R = 400 + 9 = 4099.
Vậy R = ≈688,2(mét)
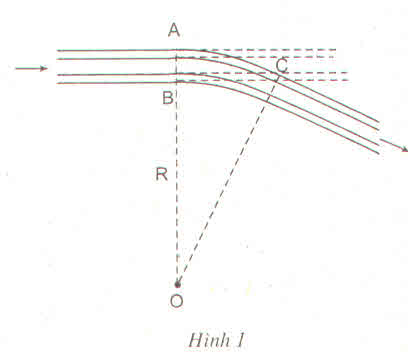
Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (h.1). Biết chiều rộng của đường ray là \(AB\approx1,1m\), đoạn \(BC\approx28,4m\). Hãy tính bán kính OA = R của đoạn đường ray hình vòng cung ?
Cho đường tròn tâm O bán kính 1,5 cm. Hãy vẽ hình vuông ABCD có 4 đỉnh nằm trên đường tròn đó. Nêu cách vẽ ?
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E
a) \(\widehat{ADC}\) và \(\widehat{ABC}\) có bằng nhau không ? Vì sao ?
b) Chứng minh CD song song với AB
c) Chứng minh AD vuông góc với OC
d) Tính số đo của \(\widehat{DAO}\)
e) So sánh hai cung BE cà CD
Cho đường tròn (0, R) và hai đường kính AB, CD vuông góc với nhau. Trên đoạn OB lấy điểm I. Tia Cl cắt đường tròn (0) tại điểm thứ hai là E. 1) Biết sđ cung DE = 50 độ. Tính số đo góc DCE và góc BOE, 2) Chứng minh 4 điểm: OIED cùng thuộc 1 đường tròn, b) Nối AE cắt CD tại H. Chứng minh: HD.IE= BI.DE
Cho nửa đường tròn (O) đường kính AB và bán kính OC ⊥ AB. Lấy điểm M thuộc cung AC . Tiếp tuyến tại M cắt OC tại N. Chứng minh rằng MNO = 2MBA
Cho đường tròn O và hai đường kính AB CD vuông góc với nhau lấy một điểm M trên cung nhỏ BC g vẽ tiếp tuyến với đường tròn O tại M tiếp tuyến này cắt CD tại S lấy điểm F thuộc cung nhỏ BC cắt AB ở E Chứng minh:
a, BD2 = DE.DF
b, góc MSD = góc MBA
Cho đường tròn O và hai đường kính AB CD vuông góc với nhau lấy một điểm M trên cung nhỏ BC g vẽ tiếp tuyến với đường tròn O tại M tiếp tuyến này cắt CD tại S lấy điểm F thuộc cung nhỏ BC cắt AB ở E Chứng minh:
a,BD mũ 2 = DE.DF
b, góc MSD = góc 2MBA
Cho nửa đường tròn đường kính AB. Lấy điểm I nằm chính giữa cung AB. Lấy điểm M trên cung BI. Kẻ IK vuông góc với AM .
a) Tinh góc AMI; Tinh góc AMB
b)Chứng minh OK là phân giác của góc MOI.
c) Chứng minh góc IAM = góc IOK
Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S.
Chứng minh rằng \(\widehat{MSD}=2\widehat{MBA}\) ?