Ta có:
![]() =
= ![]() (theo gt).
(theo gt).
![]() =
= ![]() ( vì MN // BC)
( vì MN // BC)
Suy ra ![]() =
= ![]() , do đó
, do đó ![]() =
= ![]()
Vậy ∆SMC là tam giác cân, suy ra SM = SC
Chứng minh tương tự ta cũng có ∆SAN cân , SN = SA.
Ta có:
![]() =
= ![]() (theo gt).
(theo gt).
![]() =
= ![]() ( vì MN // BC)
( vì MN // BC)
Suy ra ![]() =
= ![]() , do đó
, do đó ![]() =
= ![]()
Vậy ∆SMC là tam giác cân, suy ra SM = SC
Chứng minh tương tự ta cũng có ∆SAN cân , SN = SA.

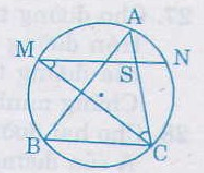
Cho ∆ABC có ba góc nhọn nội tiếp (O)Từ điểm M là điểm chính giữa
của cung AB vẽ dây MN // BC. Gọi S là giao điểm của MN với AC.Chứng
minh SM = SC và SN = SA
Mình đang cần gấp, mong các bạn giúp mình
Cho (O) đường kính AB, M là điểm chính giữa của cung AB, C là điểm bất kì thuộc cung AB sak cho C và M nằm khác phía so với AB, CM cắt AB tại D. Vẽ dây AE vuông góc với CM tại Fa/ Chứng minh ACEM là hình thang cânb/Vẽ CH vuông góc với AB. Chứng minh CH là tia phân giác góc CHO
Cho tam giác nhọn ABC nội tiếp (O). M, N, P lần lượt là điểm chính giữa của các cung AB, BC, CA. Gọi I là giao điểm của AB và MN, K là giao điểm của BP và AN, J là giao điểm của AC và PN. Chứng minh rằng:
a) ∠BKN = ∠CJN.
b) Tam giác NBK cân, tam giác IBK cân.
c) IK song song với BC, ba điểm J, K, I thẳng hàng.
Cho 2 đường tròn (O) và (O’) cắt nhau tại 2 điểm A và B. Qua A vẽ dây cung AC của đường tròn (O) cắt (O’) tại C’. Qua B vẽ dây cung BD của đường tròn (O) cắt (O’) tại D’. AC và BD cắt nhau tại I. Chứng minh DC//D’C’.
Cho đường tròn tâm O đường kính AB và S là một điểm nằm ngoài đường tròn. Vẽ đường thẳng SA và SB lần lượt cắt (O) tại điểm thứ hai M,N. Gọi H là giao điểm của AN và BM. Chứng minh rằng 1) SH ⊥ AB 2) HM . HB = HN . HA
cho A nằm ngoài đường tròn (O), đường kính BC. AB và AC cắt (O) thứ tự tạo M và N. Gọi I là giao điểm của BN và CM. chứng minh AI vuông góc với BC
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M,N. Gọi H là giao điểm của BM và AN. Chứng minh SH vuông góc với AB
Cho tam giác ABC nội tiếp đường tròn (O). Trên cung nhỏ BC của đường tròn (O), lấy điểm M. Gọi D, E, F lần lượt là hình chiếu vuông góc của M lên các đường thẳng BC, CA, AB. Chứng minh rằng ba điểm D, E, F thẳng hàng.
cho nửa đường tròn (O) có đường kính AB và điểm C thuộc nửa đường tròn đó (C khác A,B).Lấy điểm M thuộc dây BC(M khác B,C) .Tia AM cắt cung nhỏ BC tại điểm N,tia AC cắt BN tại điểm P.Cm:PCMN là tứ giác nội tiếp