Quan sát Hình 3.5 và 3.6, nhận xét về độ lớn của động năng, thế năng và cơ năng trong quá trình dao động điều hòa của vật.
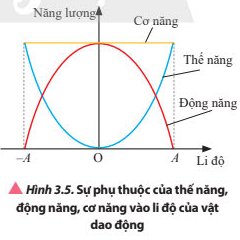
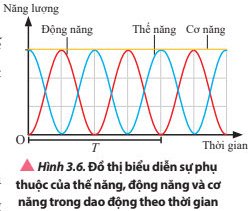
Quan sát Hình 3.5 và 3.6, nhận xét về độ lớn của động năng, thế năng và cơ năng trong quá trình dao động điều hòa của vật.


Dựa vào biểu thức (3.2) và (3.5), hãy thiết lập biểu thức (3.7).
\(W_t=\dfrac{1}{2}Kx^2=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\) (3.2)
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\) (3.5)
\(W_t+W_đ=\dfrac{1}{2}m\omega^2A^2\) (3.7)
Thảo luận (1)Hướng dẫn giảiTa có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)
(Trả lời bởi Hà Quang Minh)
Dựa vào công thức (3.5) và Hình 3.3, mô tả sự thay đổi của động năng trong một chu kì dao động của vật.
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\) (3.5)

Thảo luận (1)Hướng dẫn giảiCông thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.
(Trả lời bởi HT.Phong (9A5))
Quan sát Hình 3.5 và mô tả sự thay đổi của động năng và thế năng khi vật dao động di chuyển từ biên âm đến biên dương.

Thảo luận (1)Hướng dẫn giảiVật chuyển động từ biên âm về vị trí cân bằng thì thế năng của vật giảm từ giá trí lớn nhất về 0 còn động năng thì tăng dần từ 0 đến giá trị lớn nhất và ngược lại.
Vật chuyển động từ vị trí cân bằng đến vị trí biên âm thì thế năng của vật tăng dần từ 0 đến giá trị lớn nhất còn động năng giảm dần từ giá trị lớn nhất về 0 và ngược lại.
(Trả lời bởi Mai Trung Hải Phong)
So sánh pha dao động của thế năng và động năng khi vật dao động điều hòa.
Thảo luận (1)Hướng dẫn giảiTham khảo:
Trong quá trình vật dao động, khi động năng cực đại thì thế năng cực tiểu, khoảng thời gian ngắn nhất để chúng có cùng trạng thái là \(\Delta t=\dfrac{T}{4}\) nên độ lệch pha là\(\Delta\varphi=\dfrac{2\pi}{T}\cdot\dfrac{T}{4}=\dfrac{\pi}{2}\left(rad\right)\). Tức là động năng và thế năng vuông pha với nhau.
(Trả lời bởi HT.Phong (9A5))
Một số toà nhà cao tầng sử dụng các con lắc nặng trong bộ giảm chấn khối lượng (mass damper) để giảm thiểu sự rung động gây ra bởi gió hay những cơn địa chấn nhỏ. Giả sử vật nặng của con lắc có khối lượng 3,0.105kg, thực hiện dao động điều hoà với với tần số 15 Hz với biên độ dao động là 15 cm. Hãy xác định thế năng cực đại của hệ con lắc trong bộ giảm chấn khối lượng.
Thảo luận (1)Hướng dẫn giảiThế năng cực đại của hệ con lắc trong bộ giảm chấn khối lượng:
\(W_{tmax}=\dfrac{1}{2}mw^2A^2=\dfrac{1}{2}\cdot3\cdot10^5=3037500\pi\left(J\right)\)
(Trả lời bởi HT.Phong (9A5))
Dựa vào công thức (3.2) và Hình 3.2, mô tả sự thay đổi của thế năng trong một chu kì dao động của vật.
\(W_t=\dfrac{1}{2}Kx^2=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\) (3.2)
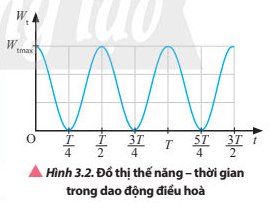
Thảo luận (1)Hướng dẫn giảiThế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.
(Trả lời bởi Mai Trung Hải Phong)
Tiến hành thí nghiệm như mô tả trong Hình 3.1. Đặt một tấm gỗ cố định lên tường, đưa vật nặng của con lắc đơn đến vị trí tiếp xúc với tấm gỗ và thả nhẹ để vật nặng bắt đầu chuyển động không vận tốc ban đầu. Khi dao động, vật nặng có và chạm vào tấm gỗ hay không? Vì sao? Trong quá trình dao động, vật nặng có những dạng năng lượng gì và sự chuyển hoá giữa chúng như thế nào?
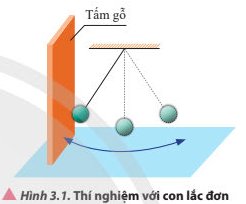
Thảo luận (1)Hướng dẫn giảiKhi dao động, vật nặng không va chạm vào tấm gỗ vì khi vật được thả với không vận tốc đầu ở vị trí biên thì vật dao động quay trở lại không thể vượt qua vị trí biên.
Trong quá trình dao động, vật nặng có những dạng năng lượng là thế năng, động năng và cơ năng, sự chuyển hóa qua lại giữa thế năng và động năng đảm bảo định luật bảo toàn cơ năng.
(Trả lời bởi Mai Trung Hải Phong)
So sánh chu kì, tần số biến thiên của thế năng với chu kì, tần số dao động của vật.
Thảo luận (1)Hướng dẫn giải`T' -` chu kì thế năng; `f' -` tần số thế năng.
`T-` chu kì dao động; `f-` tần số dao động.
Đối với `W_t` ta có: `{(T'=T/2),(f'=2f):}`
(Trả lời bởi 2611)
Một vật có khối lượng 2 kg dao động điều hoà có đồ thị vận tốc – thời gian như Hình 3.4. Xác định tốc độ cực đại và động năng cực đại của vật trong quá trình dao động.
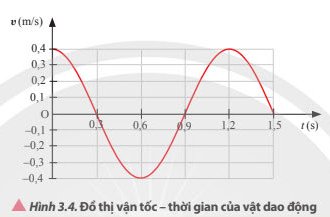
Thảo luận (1)Hướng dẫn giảiTốc độ cực đại của vật trong quá trình dao động là 0,4 m/s
Thế năng cực đại của vật trong quá trình dao động là
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.0,4^2=0,16\left(J\right)\).
(Trả lời bởi Mai Trung Hải Phong)