`T' -` chu kì thế năng; `f' -` tần số thế năng.
`T-` chu kì dao động; `f-` tần số dao động.
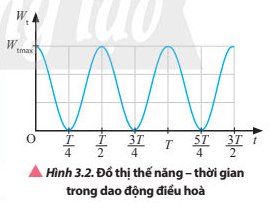
Đối với `W_t` ta có: `{(T'=T/2),(f'=2f):}`
`T' -` chu kì thế năng; `f' -` tần số thế năng.
`T-` chu kì dao động; `f-` tần số dao động.
Đối với `W_t` ta có: `{(T'=T/2),(f'=2f):}`
Một hệ dao động điều hoà với chu kì 2 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ hai?
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng theo chiều âm của trục toạ độ. Chọn gốc thế năng tại vị trí cân bằng của vật. Hãy vẽ phác đồ thị thể hiện sự phụ thuộc vào thời gian của động năng và thế năng trong hai chu kì dao động trên cùng một hệ trục toạ độ. Chỉ ra trên đồ thị những thời điểm mà động năng và thế năng có độ lớn bằng nhau.
Xét một vật bắt đầu dao động điều hoà từ vị trí cân bằng, hãy chỉ ra những khoảng thời gian trong một chu kì dao động mà:
a) thế năng tăng dần trong khi động năng giảm dần.
b) thế năng giảm dần trong khi động năng tăng dần.
Dựa vào công thức (3.2) và Hình 3.2, mô tả sự thay đổi của thế năng trong một chu kì dao động của vật.
\(W_t=\dfrac{1}{2}Kx^2=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\) (3.2)
So sánh pha dao động của thế năng và động năng khi vật dao động điều hòa.
Dựa vào công thức (3.5) và Hình 3.3, mô tả sự thay đổi của động năng trong một chu kì dao động của vật.
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\) (3.5)

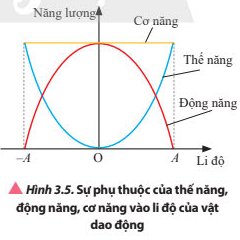
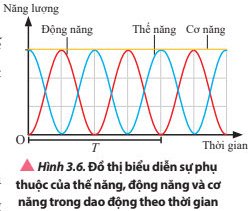
Quan sát Hình 3.5 và 3.6, nhận xét về độ lớn của động năng, thế năng và cơ năng trong quá trình dao động điều hòa của vật.
Biết phương trình li độ của một vật có khối lượng 0,2 kg dao động điều hoà là x = 5cos(20t) (cm).
a) Tính cơ năng trong quá trình dao động.
b) Viết biểu thức thế năng và động năng.
Quan sát Hình 3.5 và mô tả sự thay đổi của động năng và thế năng khi vật dao động di chuyển từ biên âm đến biên dương.
