Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.
Bài 3. Hai mặt phẳng vuông góc
Giải mục 3 trang 67, 68, 69 (SGK Chân trời sáng tạo)
Thảo luận (1)
Giải mục 4 trang 69, 70, 71 (SGK Chân trời sáng tạo)
a) Cho hình lăng trụ ABCDE.ABCDE có cạnh bên AA vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuôn...
Đọc tiếp
a) Cho hình lăng trụ \(ABCDE.A'B'C'D'E'\) có cạnh bên \(AA'\) vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?
c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?
d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hinh 18d) thì có bao nhiêu mặt là hình chữ nhật?
Thảo luận (1)Hướng dẫn giảia: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
b: Các mặt bên của hình lăng trụ này vừa là hình chữ nhật, vừa vuông góc với đáy
c: Có 4 mặt bên là hình chữ nhật
d: Có tất cả là 6 mặt là hình chữ nhật
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Giải mục 2 trang 66, 67 (SGK Chân trời sáng tạo)
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.

Thảo luận (1)Hướng dẫn giảiB1: Đặt êke sao cho hai cạnh góc vuông của hai êke chạm vào nhau tạo thành một đường thẳng, hai cạnh còn lại của hai êke sát với mặt sàn.
B2: Nếu đường thẳng đó nằm sát với bức tường thì bức tường vuông góc với mặt sàn.
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Giải mục 3 trang 67, 68, 69 (SGK Chân trời sáng tạo)
Tứ diện ABCD có AB bot left( {BCD} right). Trong tam giác BCD vẽ đường cao BE và DF cắt nhau tại O. Trong mặt phẳng left( {ACD} right) vẽ {rm{D}}K vuông góc với AC tại K. Gọi H là trực tâm của tam giác ACD. Chứng minh rằng:a) left( {ADC} right) bot left( {ABE} right) và left( {ADC} right) bot left( {DFK} right);b) OH bot left( {ADC} right).
Đọc tiếp
Tứ diện \(ABCD\) có \(AB \bot \left( {BCD} \right)\). Trong tam giác \(BCD\) vẽ đường cao \(BE\) và \(DF\) cắt nhau tại \(O\). Trong mặt phẳng \(\left( {ACD} \right)\) vẽ \({\rm{D}}K\) vuông góc với \(AC\) tại \(K\). Gọi \(H\) là trực tâm của tam giác \(ACD\). Chứng minh rằng:
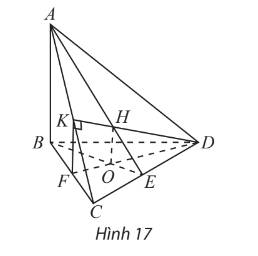
a) \(\left( {ADC} \right) \bot \left( {ABE} \right)\) và \(\left( {ADC} \right) \bot \left( {DFK} \right)\);
b) \(OH \bot \left( {ADC} \right)\).
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)\)
Lại có \(C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {ABE} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}\)
Lại có \(AC \subset \left( {A{\rm{D}}C} \right)\)
Vậy \(\left( {ADC} \right) \bot \left( {DFK} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 3 trang 67, 68, 69 (SGK Chân trời sáng tạo)
Cho đường thẳng a vuông góc với mặt phẳng left( Q right). Mặt phẳng left( P right) chứa a và cắt left( Q right) theo giao tuyến c. Trong left( Q right) ta vẽ đường thẳng b vuông góc với c. Hỏi:a) left( P right) có vuông góc với left( Q right) không?b) Đường thẳng b vuông góc với left( P right) không?
Đọc tiếp
Cho đường thẳng \(a\) vuông góc với mặt phẳng \(\left( Q \right)\). Mặt phẳng \(\left( P \right)\) chứa \(a\) và cắt \(\left( Q \right)\) theo giao tuyến \(c\). Trong \(\left( Q \right)\) ta vẽ đường thẳng \(b\) vuông góc với \(c\).

Hỏi:
a) \(\left( P \right)\) có vuông góc với \(\left( Q \right)\) không?
b) Đường thẳng \(b\) vuông góc với \(\left( P \right)\) không?
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 2 trang 66, 67 (SGK Chân trời sáng tạo)
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Thảo luận (1)Hướng dẫn giảiGọi O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
a:S.ABCD là hình chóp tứ giác đều nên SO vuông góc (ABCD)
mà \(SO\subset\left(SAC\right)\)
nên \(\left(SAC\right)\perp\left(ABCD\right)\)
b: BD vuông góc SO
BD vuông góc AC
\(SO,AC\subset\left(SAC\right)\)
=>\(BD\perp\left(SAC\right)\)
=>\(\left(SAC\right)\perp\left(SBD\right)\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Giải mục 2 trang 66, 67 (SGK Chân trời sáng tạo)
Từ một điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\) lần lượt vuông góc với hai bức tường trong phòng. Đo góc \(xOy\).
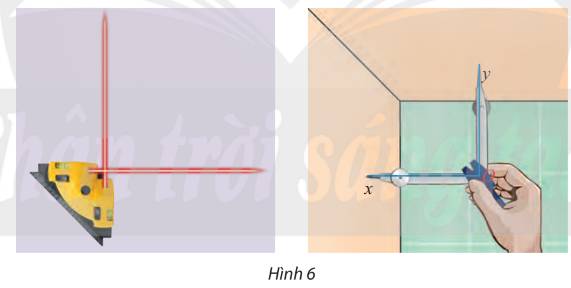
Thảo luận (1)Hướng dẫn giải\(\widehat{xOy}=90^0\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Giải mục 1 trang 65 (SGK Chân trời sáng tạo)
a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng left( Q right) và mặt đất left( P right).
Đọc tiếp
a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?
b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng \(\left( Q \right)\) và mặt đất \(\left( P \right)\).
Thảo luận (1)Hướng dẫn giảia: Có thể xác định được bằng cách bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh.
b: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
Khi đặt thiết bị lên mp nghiêng (Q) thì ta sẽ có:
\(OM\perp\left(Q\right);ON\perp\left(P\right)\)
\(OM\subset\left(P\right),ON\subset\left(Q\right)\)
=>\(\widehat{\left(P\right),\left(Q\right)}=\widehat{\left(OM;ON\right)}=\widehat{MON}=90^0\)
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Giải mục 2 trang 66, 67 (SGK Chân trời sáng tạo)
Cho hai mặt phẳng left( P right) và left( Q right) cắt nhau theo giao tuyến d điểm M không thuộc left( P right) và left( Q right). Gọi H và K lần lượt là hình chiếu vuông góc của M lên left( P right) và left( Q right). Gọi O là giao điểm của d và left( {MHK} right) (Hình 8). a) Giả sử left( P right) bot left( Q right), hãy cho biết tứ giác MHOK là hình gì? Tìm trong left( P right) đường thẳng vuông góc với left( Q right).b) Giả sử left( P right) chứa đường thẳng a với a bot left( Q right), hãy c...
Đọc tiếp
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).
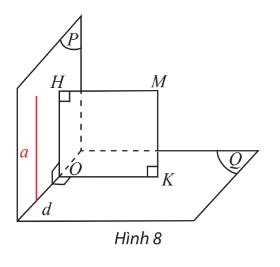
a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot OH\\MK \bot \left( Q \right) \Rightarrow MK \bot OK\\\left( {\left( P \right),\left( Q \right)} \right) = {90^ \circ } \Rightarrow \left( {MH,MK} \right) = {90^ \circ } \Rightarrow MH \bot MK\end{array}\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HMK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Trong \(\left( P \right)\) có đường thẳng \(OH\) vuông góc với \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right) \Rightarrow a \bot OK\\MH \bot \left( P \right) \Rightarrow MH \bot a\end{array} \right\} \Rightarrow MH\parallel OK\)
Lại có \(MH \bot \left( P \right)\). Vậy \(OK \bot \left( P \right) \Rightarrow OK \bot OH\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HOK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
\(\left( {\left( P \right),\left( Q \right)} \right) = \left( {MH,MK} \right) = \widehat {HMK} = {90^ \circ }\).
(Trả lời bởi Quoc Tran Anh Le)
Giải mục 3 trang 67, 68, 69 (SGK Chân trời sáng tạo)
Cho hai mặt phẳng left( P right) và left( Q right) cùng vuông góc với mặt phẳng left( R right). Gọi a là giao tuyến của left( P right) và left( Q right). Lấy điểm M trong left( R right), vẽ hai đường thẳng MH và MK lần lượt vuông góc với left( P right) và left( Q right). Hỏi: a) Hai đường thẳng MH và MK có nằm trong left( R right) không?b) Đường thẳng a có vuông góc với left( R right) không?
Đọc tiếp
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\). Lấy điểm \(M\) trong \(\left( R \right)\), vẽ hai đường thẳng \(MH\) và \(MK\) lần lượt vuông góc với \(\left( P \right)\) và \(\left( Q \right)\). Hỏi:
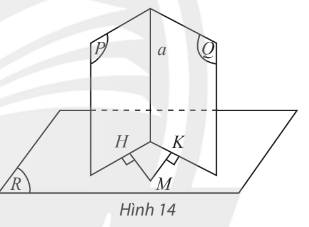
a) Hai đường thẳng \(MH\) và \(MK\) có nằm trong \(\left( R \right)\) không?
b) Đường thẳng \(a\) có vuông góc với \(\left( R \right)\) không?
Thảo luận (1)Hướng dẫn giảia) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)
(Trả lời bởi Quoc Tran Anh Le)