Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).
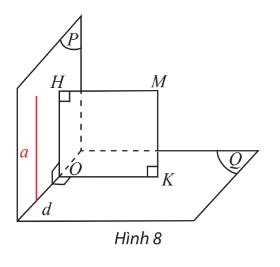
a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).
a) Ta có:
\(\begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot OH\\MK \bot \left( Q \right) \Rightarrow MK \bot OK\\\left( {\left( P \right),\left( Q \right)} \right) = {90^ \circ } \Rightarrow \left( {MH,MK} \right) = {90^ \circ } \Rightarrow MH \bot MK\end{array}\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HMK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Trong \(\left( P \right)\) có đường thẳng \(OH\) vuông góc với \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right) \Rightarrow a \bot OK\\MH \bot \left( P \right) \Rightarrow MH \bot a\end{array} \right\} \Rightarrow MH\parallel OK\)
Lại có \(MH \bot \left( P \right)\). Vậy \(OK \bot \left( P \right) \Rightarrow OK \bot OH\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HOK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
\(\left( {\left( P \right),\left( Q \right)} \right) = \left( {MH,MK} \right) = \widehat {HMK} = {90^ \circ }\).