Cho các số \( - 7;\,0,5; 0;1\frac{2}{3}\). Với mỗi số, hãy viết một phân số bằng số đã cho.
Bài 1. Tập hợp các số hữu tỉ
Hoạt động 1 (SGK Chân trời sáng tạo trang 6)
Thảo luận (1)
Thực hành 1 (SGK Chân trời sáng tạo trang 6)
Vì sao các số \( - 0,33;\,0;\,3\frac{1}{2};\,0,25\) là các số hữu tỉ?
Thảo luận (2)Hướng dẫn giảiCác số \( - 0,33;\,0;\,3\frac{1}{2};\,0,25\) là các số hữu tỉ vì:
\(\begin{array}{l} - 0,33 = \frac{{-33}}{{100}} = \frac{{-99}}{{300}} = ....\\0 = \frac{0}{1} = \frac{0}{2} = ...\\3\frac{1}{2} = \frac{7}{2} = \frac{{ - 7}}{{ - 2}} = ...\\0,25 = \frac{{25}}{{100}} = \frac{1}{4} = ...\end{array}\
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Chân trời sáng tạo trang 6)
Viết các số đo các đại lượng sau dưới dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},\,\,b \ne 0.\)
a) \(2,5\)kg đường
b) \(3,8\) m dưới mực nước biển
Thảo luận (1)Hướng dẫn giảia) \(2,5\,\,kg = \frac{{25}}{{10}}\,\,kg\, = \,\frac{5}{2}\,kg\)
b) \(3,8\,m = \frac{{38}}{{10}}\,m\, = \frac{{19}}{5}\,m\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Chân trời sáng tạo trang 6,7)
a) So sánh hai phân số \(\frac{2}{9}\) và \( - \frac{5}{9}\).
b) Trong mỗi trường hợp sau, nhiệt độ nào cao hơn?
i) \({0^o}C\) và \( - 0,{5^o}C;\) ii) \( - {12^o}C\) và \( - {7^o}C\).
Thảo luận (1)Hướng dẫn giảia) Ta có: \(2 > - 5\) nên \(\frac{2}{9} > \frac{{ - 5}}{9}\)hay \(\frac{2}{9} > - \frac{5}{9}\).
b) Ta có:
i) \(0 > - 0,5\) nên \({0^o}C > - 0,{5^o}C;\)
ii) Do \(12 > 7\) nên \( - 12 < - 7\). Do đó, \( - {12^o}C < - {7^o}C\).
(Trả lời bởi Hà Quang Minh)
Thực hành 2 (SGK Chân trời sáng tạo trang 6,7)
Cho các số hữu tỉ: \(\frac{{ - 7}}{{12}};\,\frac{4}{5};\,5,12;\, - 3;\,\frac{0}{{ - 3}};\, - 3,75.\)
a) So sánh \(\frac{{ - 7}}{{12}}\) với \( - 3,75\); \(\frac{0}{{ - 3}}\) với \(\frac{4}{5}\).
b) Trong các số hữu tỉ đã cho, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?
Thảo luận (1)Hướng dẫn giảia) +) Ta có: \( - 3,75 = \frac{{ - 375}}{{100}} = \frac{{ - 15}}{4} = \frac{{ - 45}}{{12}}\).
Do \( - 7 > - 45\) nên \(\frac{{ - 7}}{{12}} > \frac{{ - 45}}{{12}}\).
+) Ta có: \(\frac{0}{{ - 3}} = 0\). Nên \(\frac{0}{{ - 3}} < \frac{4}{5}\).
b) Các số hữu tỉ dương là: \(\frac{4}{5};\,5,12\).
Các số hữu tỉ âm là: \(\frac{{ - 7}}{{12}};\, - 3;\, - 3,75\)
Do \(\frac{0}{{ - 3}} = 0\) nên số không là số hữu tỉ dương cũng không là số hữu tỉ âm là: \(\frac{0}{{ - 3}}\).
(Trả lời bởi Hà Quang Minh)
Hoạt động 3 (SGK Chân trời sáng tạo trang 6,7)
a) Biểu diễn các số nguyên -1;1;-2 trên trục số.
b) Quan sát Hình 2. Hãy dự đoán điểm A biểu diễn số hữu tỉ nào?
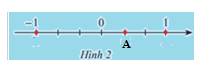
Thảo luận (2)Hướng dẫn giảiđiểm A biểu diễn \(\dfrac{1}{3}\)
(Trả lời bởi Vũ Quang Huy)
Thực hành 3 (SGK Chân trời sáng tạo trang 6,7)
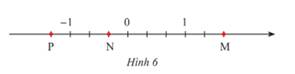
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
Thảo luận (3)Hướng dẫn giảia) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)
(Trả lời bởi Kiều Sơn Tùng)
Hoạt động 4 (SGK Chân trời sáng tạo trang 8,9)
Em có nhận xét gì về vị trí điểm \(\frac{{ - 4}}{3}\) và \(\frac{4}{3}\) trên trục số (Hình 7) so với điểm 0?
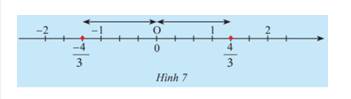
Thảo luận (2)Hướng dẫn giảiHai điểm này cách đều số 0 trên trục số
(Trả lời bởi Nguyễn Lê Phước Thịnh)
Thực hành 4 (SGK Chân trời sáng tạo trang 8,9)
Tìm số đối của mỗi số sau: \(7;\frac{{ - 5}}{9};-0,75;\,0;\,1\frac{2}{3}\).
Thảo luận (1)Hướng dẫn giảiSố đối của các số \(7;\frac{{ - 5}}{9};-0,75;\,0;\,1\frac{2}{3}\) lần lượt là: \( - 7;\frac{5}{9};0,75;\,0;\, - 1\frac{2}{3}\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Chân trời sáng tạo trang 8,9)
Bạn Hồng đã phát biểu: “4,1 lớn hơn 3,5. Vì thế – 4,1 cũng lớn hơn -3,5”.
Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?
Thảo luận (2)Hướng dẫn giảiDo \(4,1 > 3,5\) nên \( - 4,1 < - 3,5\). Vì vậy phát biểu của bạn Hồng là sai.
(Trả lời bởi Hà Quang Minh)
