Cho tam giác ABC nhọn nội tiếp đường tròn (O). 2 đường cao BD, CE cắt nhau tại H . Vẽ đường kính AF
a) BFCH là hình gì ? cm
b) gọi M là trung điểm BC. cm : M,H,F thẳng hàng
c) cm: AH = 2.OM
Cho tam giác ABC nhọn nội tiếp đường tròn (O). 2 đường cao BD, CE cắt nhau tại H . Vẽ đường kính AF
a) BFCH là hình gì ? cm
b) gọi M là trung điểm BC. cm : M,H,F thẳng hàng
c) cm: AH = 2.OM
Cho tam giác ABC nội tiếp đưòng tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF
a, Tứ giác BFCH là hình gì?
b, Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H, M, F thẳng hàng
c, Chứng minh OM = 1 2 AH
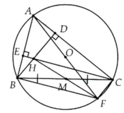
a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB đồng dạng với ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
b: Xét (O) có
ΔABF nội tiếp
AF là đường kính
Do đó: ΔABF vuông tại B
=>BF vuông góc AB
mà CH vuông góc AB
nên BF//CH
Xét (O) có
ΔACF nội tiếp
AF là đường kính
Do đó: ΔACF vuông tại C
=>AC vuông góc CF
mà AC vuông góc BH
nên BH//CF
Xét tứ giác BHCF có
BH//CF
BF//CH
Do đó: BHCF là hình bình hành
c: BHCF là hình bình hành
=>BC cắt HF tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HF
=>H,M,F thẳng hàng
Cho ∆ ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD và CE cắt nhau tại H, đường kính AF, gọi G là trọng tâm ∆ABC.
a, cm BH//FC
b, cm BHCF là hbh
c, Vẽ OM vuông góc BC tại M cm H,M,F thẳng hàng
d, gọi G là trọng tâm ∆ABC. cm S ∆ahg = 2S ∆ago
Giúp em phần d với ạ
Tham khảo:
d: Xét ΔAHF có FO/FA=FM/FH=1/2
nên OM//AH và OM/AH=FO/FA=1/2
Gọi giao cuảt AG với OH là G'
OM//AH
=>AG'/G'M=HG'/G'O=AH/OM=2
G là trọng tâm của ΔABC
=>AG/GM=2
=>AG'/G'M=AG/GM
=>G' trùng với G
=>HG=2GO
=>S AHG=2*S AGO
Cho tam giác ABC nhọn nội tiếp (O), có BE , CF là 2 đường cao cắt nhau tại H
a) Cm: tứ giác BEFC nội tiếp, xác định vị trí tâm I của đường tròn đó.
b) vẽ AK là đường kính của (O). Cm: H, I, K thẳng hàng
c) gọi D là giao điểm của AH và BC. Cm 4 điểm : D,E,F,I cùng thuộc 1 đường tròn
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
I là trung điểm của BC
b: góc ABK=1/2*sđ cung AK=90 độ
=>BK//CH
góc ACK=1/2*sđ cung AK=90 độ
=>CK//BH
mà BK//CH
nên BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>H,I,K thẳng hàng
cho tam giác abc nội tiếp đường tròn tâm o bd và ce là hai đường cao cắt nhau tại h , af là đường kính , m là trung điểm của bc
cm 3 điểm h , m , f thằng hàng
om = 1/2 ah
cho tam giác nhọn ABC nội tiếp đường tròn (O;R) (AB>AC ) . gọi H là giao điểm của 2 đường cao BD và CE của tam giác ABC , F là giao điểm của AH và BC .a) CM tứ giác BEHF nội tiếp . b) CM FA*FH =FB *FC . vẽ đường kính AI của đường tròn (O) . gọi K là điểm đối xứng của H qua BC . CM tứ giác BIKC là hình thang cân
Bài 1: Cho tam giác ABC (AB < AC ) có 3 góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE; F là giao điểm của AH và BC
a) CM: Tứ giác AEHD nội tiếp đường tròn
b) Gọi M là trung điểm của AH. CM: MD là tiếp tuyến của đg tròn (O)
c) Gọi K là giao điểm của AH và DE. CM: MD2 = MK.MF và K là trực tâm của tam giác MBC
d) CM: 2/FK = 1/FH + 1/FA
cho tam giác ABC ( AB < AC) có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BD, CE của tam giác ABC cắt nhau tại H.
1. Cm tg AEDH, BCDE nội tiếp
2. Cm OA vuông góc với DE
3. Đường tròn đường kính AH cắt đt (O) tại F ( F khác A). cm các đường thẳng DE, BC, AF đồng duy
Em chỉ cần câu 3 thôi ạ, em cảm ơn