Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác.

a)Một chiếc đèn thả trần có dạng hình chóp tam giác đều có tất cả các cạnh đều khoảng 20cm.Độ dài trung đoạn khoảng 17,32cm.Tính diện tích xung quanh của chiếc đèn thả trần đó
b)Cho hình chóp tam giác đều S.ABC có cạnh đấy bằng 4cm và chiều cao tam giác đáy là 3,5cm,trung đoạn bằng 5 cm.Tính diện tích xung quanh và diện tích toàn phần (tức là tổng diện tích các mặt) của hình chóp
giúp mình với ạ
a: Chu vi đáy là 20*3=60(cm)
Diện tích xung quanh là \(17.32\cdot60=1039.2\left(cm^2\right)\)
b: Chu vi đáy là \(4\cdot3=12\left(cm\right)\)
Diện tích đáy là \(\dfrac{1}{2}\cdot3.5\cdot4=7\left(cm^2\right)\)
Diện tích xung quanh là \(12\cdot5=60\left(cm^2\right)\)
Diện tích toàn phần là \(60+7=67\left(cm^2\right)\)
Tại ba đỉnh của một tam giác đều cạnh a = 3 cm trong không khí, người ta lần lượt đặt ba điện tích điểm q 1 = q 2 = - 2 . 10 - 10 C v à q 3 = 2 . 10 - 10 C . Xác định độ lớn của cường độ điện trường tại tâm O của tam giác.
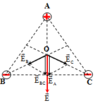
E → O = E → A + E → B + E → C = E → A + E → B C → E → A ↑ ↑ E → B C E O = E A + E B C
Trong đó: E A = E B C = k q O A 2 → O A = 2 3 a 2 − a 2 2 = 9.10 3 V m
→ E → A ↑ ↑ E → B C E O = E A + E B C = 18.10 3
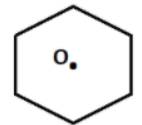
Người ta muốn đặt một trạm biến áp để đưa điện về sáu ngôi nhà. Phải đặt trạm biến áp ở đâu để khoảng cách từ trạm biến áp đến sáu ngôi nhà bằng nhau, biết rằng sáu ngôi nhà ở vị trí sáu đình của hình lục giác đều?
Phải đặt trạm biến áp ở tâm O hình lục giác đều tạo bởi sáu ngôi nhà vì O cách đều 6 ngôi nhà.
Hai điện tích q 1 = q 2 = 6 , 4 . 10 - 10 C , đặt tại 2 đỉnh B và C của một tam giác đều ABC có cạnh bằng 8 cm, trong không khí. Gọi M là điểm nằm trên đường trung trực của BC, x là khoảng cách từ M đến BC. Xác định x để cường độ điện trường tổng hợp tại M lớn nhất.
A . x = 2 2 c m
B. x = 4 cm
C. x = 2 cm
D. x = 0
một bóng đèn nhỏ s, được xem là nguồn sáng điểm đặt cach bức tường một khoảng sh =1m. tại trung điểm m của sh ta đặt một tâms bìa hình tròn có bán kính 20cm và song song với tường.
a) vẽ hình xác định đường kính bóng tối trên tường.
b)giữ nguyên vị trí tấm bìa, dịch chuyển nguồn sáng về gần với tường thì đường kính bống tối tăng hay giảm?
một bóng đèn nhỏ s, được xem là nguồn sáng điểm đặt cach bức tường một khoảng sh =1m. tại trung điểm m của sh ta đặt một tâms bìa hình tròn có bán kính 20cm và song song với tường.
a) vẽ hình xác định đường kính bóng tối trên tường.
b)giữ nguyên vị trí tấm bìa, dịch chuyển nguồn sáng về gần với tường thì đường kính bống tối tăng hay giảm?
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
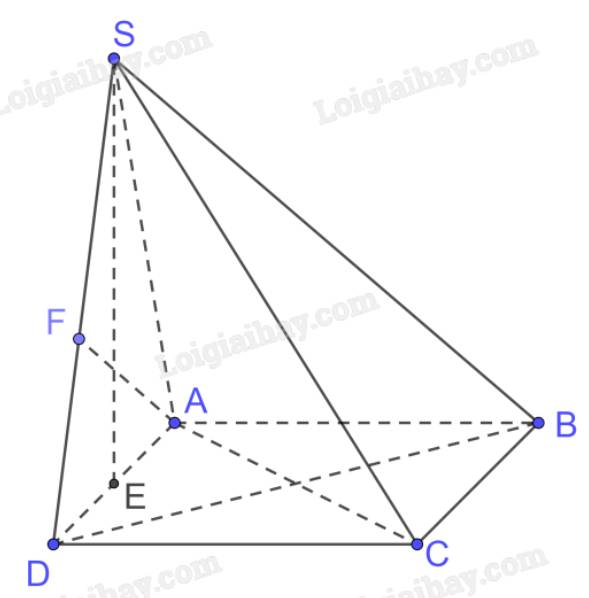
a) Gọi E là trung điểm của AD
\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)
Mà tam giác SAD đều
\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)
Xét tam giác SDE vuông tại E có
\(SE = \sqrt {S{D^2} - D{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)
Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)
\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a
c) Trong (SAD) kẻ \(AF \bot SD\)
Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)
\( \Rightarrow \) d(AB, SD) = AF
Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)
Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)
Cho hình chóp tam giác đều S.ABC có SA=a , A S B ⏞ = 30 ° Người ta muốn trang trí cho hình chóp bằng một dây đèn nháy chạy theo các điểm A, M, N rồi quay lại A (đúng một vòng) như hình bên dưới. Độ dài ngắn nhất của dây đèn nháy là:
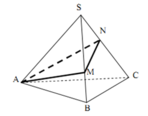
A. a 2 2
B. a 2
C. a 3
D. a 3 3
Đáp án B
Trải hình ra ta thu được:
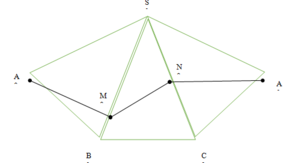
Dễ thấy AM + MN + NA đạt giá trị nhỏ nhất khi A, M, N, A thẳng hàng
Lại có S.ABC là hình chóp tam giác đều
ð ∆SAB = ∆SBC = ∆SAC (c.c.c)
⇒ AS B ^ = B S C ^ = C S A ^ ⇒ AS A ^ = 90 °
AM + MN + N A m i n = a 2
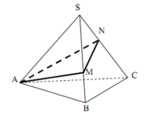
Cho hình chóp tam giác đều S.ABC có SA = a, A S B ^ = 30 0 . Người ta muốn trang trí cho hình chóp bằng một dây đèn nháy chạy theo các điểm A, M, N rồi quay lại A (đúng một vòng) như hình bên dưới. Độ dài ngắn nhất của dây đèn nháy là:
A . a 2 2
B . a 2
C . a 3
D . a 3 3
Đáp án B
Dễ thấy AM + MN + NA đạt giá trị nhỏ nhất khi A, M, N, A thẳng hàng
Lại có S.ABC là hình chóp tam giác đều
=> ∆SAB = ∆SBC = ∆SAC (c.c.c)
=> AM + MN + NA min = a 2
Một lều trại có dạng hình lăng trụ đứng đặt nằm ngang. Đáy của hình lăng trụ (tức hai đầu hổi của lều) có hình dạng là các tam giác cân, cạnh đáy của các tam giác cân này tiếp giáp mặt đâ't và có độ dài 3 m, chiều cao tương ứng dài 2m. Chiều cao lăng trụ (tức chiều dài của lều trại) bằng 4m.
a) Tính diện tích bạt phủ hai mái lều.
b) Tính thê tích của lều trại
a) Tính được diện tích bạt phủ 2 mái lều: 20 (m2)
b) Thể tích của leeud trại là: V = 12 (m3)