Question

Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).

a) Tính chiều cao của hình chóp.

b) Tính khoảng cách giữa BC và (SAD).

c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.

Answer 1

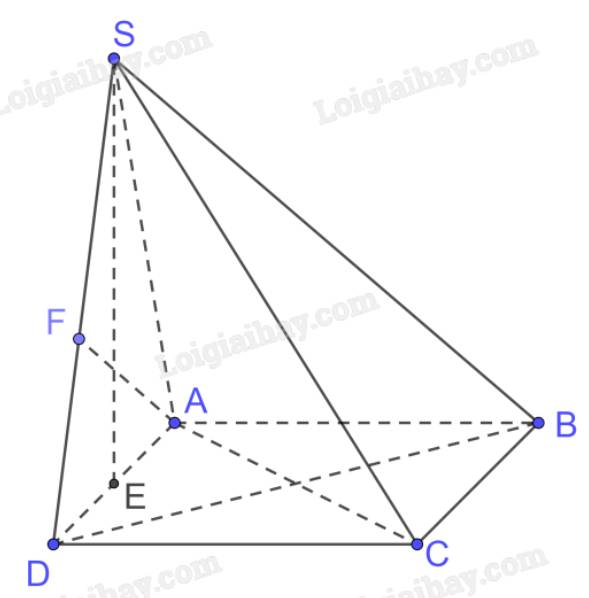
a) Gọi E là trung điểm của AD

\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)

Mà tam giác SAD đều

\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)

Xét tam giác SDE vuông tại E có

\(SE = \sqrt {S{D^2} - D{E^2}}  = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\)

b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)

Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)

\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a

c) Trong (SAD) kẻ  \(AF \bot SD\)

Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)

\( \Rightarrow \) d(AB, SD) = AF

Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)

Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)