SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:20
Bài 26. Khoảng cách
Các câu hỏi tương tự
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:19
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ⊥ (ABCD).
a) Tính chiều cao của hình chóp.
b) Tính khoảng cách giữa BC và (SAD).
c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:18
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right),SA = a\sqrt 2 .\)
a) Tính khoảng cách từ A đến SC.
b) Chứng minh \(BD \bot \left( {SAC} \right).\)
c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:21
Cho hình lập phương ABCD.A'B'C'D' có cạnh a.
a) Chứng minh rằng hai mặt phẳng (D'AC) và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm E, F của DB' với (D'AC),(BC'A'). Tính d((D'AC), (BC'A')).
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:16
Cho hình chóp S.ABC có SA \( \bot \) (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP),(ABC)) và d(NP,(ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A,(SBC)).
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:18
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).a) Mặt phẳng chứa a và a có vuông góc với (Q) hay không?b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.
Đọc tiếp
Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).
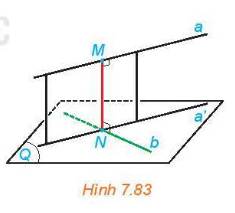
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?
b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?
c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:14
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M, N bất kì thuộc a và gọi A, B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:20
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:16
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 150 so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?
Đọc tiếp
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 150 so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:13
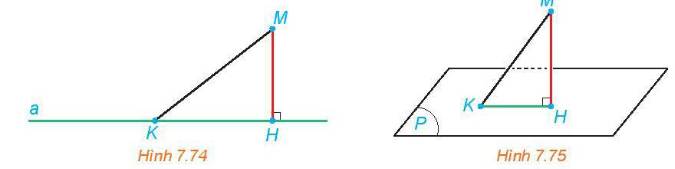
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).
