a) Xét tứ giác BCB'C' có 

\(\widehat{BC'C}=\widehat{BB'C}\left(=90^0\right)\)

\(\widehat{BC'C}\) và \(\widehat{BB'C}\) là hai góc cùng nhìn cạnh BC

Do đó: BCB'C' là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Tham khảo:

a: Xét tứ giác BHCK có

I là trung điểm chung của BC và HK

=>BHCK là hình bình hành

b: BHCK là hbh

=>BH//CK và BK//CH

=>BK vuông góc AB và CK vuông góc CA

góc ABK=góc ACK=90 độ

=>ABKC nội tiếp đường tròn đường kính AK

=>O là trung điểm của AK

c: Xét ΔKAH có

KO/KA=KI/KH=1/2

nên OI//AH

d: gọi giao của AH với BC là F

=>AH vuông góc BC tại F

Xét ΔBEC vuông tại E và ΔBFA vuông tại F có

góc B chung

=>ΔBEC đồng dạng với ΔBFA

=>BE/BF=BC/BA

=>BE*BA=BF*BC

Xét ΔCDB vuông tại D và ΔCFA vuông tại F có

góc C chung

=>ΔCDB đồng dạng với ΔCFA

=>CD/CF=CB/CA
=>CD*CA=CF*CB

=>BE*BA+CD*CA=BC^2

Bài 1 :                                                      Bài giải

Hình tự vẽ //                                       

a) Ta có DOC = cung DC

Vì DOC là góc ở tâm và DAC là góc chắn cung DC

=>DOC = 2 . AOC (1)

mà tam giác AOC cân =>AOC=180-2/AOC (2)

Từ (1) ; (2) ta được DOC + AOC = 180

b) Góc ACD là góc nội tiếp chắn nữa đường tròn

=>ACD=90 độ

c) c) HC=1/2*BC=12

=>AH=căn(20^2-12^2)=16

Ta có Sin(BAO)=12/20=>BAO=36.86989765

=>AOB=180-36.86989765*2=106.2602047

Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)

<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2

=>OA=12.5

a: R=HC/2=6,4:2=3,2(cm)

Ta có: = 2 = 2.60^o = 120^o (1)

(góc nội tiếp và góc ở tâm cùng chắn một cung)

và = (đối đỉnh)

mà = 180^o - = 180^o - 60^o = 120^o

nên = 120^{o (2)}

= +

= 60^o + = 60^o+ 60^o

(sử dụng góc ngoài của tam giác)

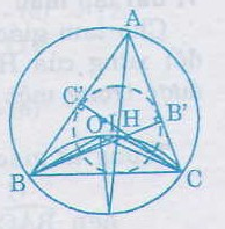
Do đó = 120^o

Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120^o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn

Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60^o = 120^o (1)

(góc nội tiếp và góc ở tâm cùng chắn một cung)

và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)

mà \(\widehat{B'HC'}\) = 180^o - \(\widehat{A}\) = 180^o - 60^o = 120^o

nên \(\widehat{BHC}\) = 120^{o (2)}

\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)

= 60^o + \(\dfrac{180^0-60^0}{2}\) = 60^o+ 60^o

(sử dụng góc ngoài của tam giác)

Do đó \(\widehat{BIC}\) = 120^o

Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120^o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn