Cho S1, S2 là diện tích các hình phẳng được mô tả trong Hình 3. Tính \(\dfrac{S_1}{S_2}\).

Cho ΔABC có AB=3cm;AC=4cm;BC=5cm , gọi AD là phân giác góc BAC.Gọi S1 và S2 lần lượt là diện tích ΔABD và ΔACD . Tính tỉ số \(\dfrac{S_1}{S_2}\)
A.\(\dfrac{S_1}{S_2}\)=\(\dfrac{4}{3}\) B.\(\dfrac{S_1}{S_2}\)=\(\dfrac{2}{3}\) C.\(\dfrac{S_1}{S_2}\)=\(\dfrac{3}{4}\) D.\(\dfrac{S_1}{S_2}\)=\(\dfrac{3}{2}\)
Giải thích vắn tắt giúp em là được ạ
Cho ΔABC có AB=3m;AC=4cm;BC=5cm.Gọi AD là phân giác của góc BAC.Gọi S1;S2 lần lượt là diện tích ΔABD và ΔACD.Tính tỉ số \(\dfrac{S_1}{S_2}\)
A.\(\dfrac{S_1}{S_2}\)=\(\dfrac{4}{3}\) B.\(\dfrac{S_1}{S_2}\)=\(\dfrac{2}{3}\) C.\(\dfrac{S_1}{S_2}\)=\(\dfrac{3}{4}\) D.\(\dfrac{S_1}{S_2}\)=\(\dfrac{3}{2}\)
trong một máy nén thủy lực, gọi F1,F2 lần lượt là lực tác dụng lên pít tông lớn, nhỏ; S1, S2 lần lượt là diện tích pít tông lớn, nhỏ thì biểu thức nào sau đây đúng:
A.\(\dfrac{F_1}{F_2}=\dfrac{S_1}{S_2}\)
B.\(\dfrac{F_1}{F_2}=\dfrac{S_2}{S_1}\)
C.\(\dfrac{F_1}{S_2}=\dfrac{F_1}{S_1}\)
D.\(F_1=F_2.\dfrac{S_2}{S_1}\)
Cho tam giác ABC các góc đều nhọn. Các đường cao AA', BB', CC' cắt nhau tại H. Gọi S1, S2, S3 lần lượt là diện tích các tam giác AB'C', BC'A', CA'B'. CM: \(\dfrac{S_1}{AH^2}=\dfrac{S_2}{BH^2}=\dfrac{S_3}{CH^2}\)
Cho hình phẳng giới hạn bởi các đường y = sin x , y = cos x và S1, S2 là diện tích của các phần được gạch chéo như hình vẽ. Tính S 1 2 + S 2 2 .
![]()
![]()
![]()
![]()
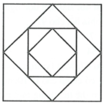
Cho hình vuông có cạnh là 1. Nối các trung điểm của hình vuông trên ta được một hình vuông có diện tích S 1 tiếp tục quá trình trên với các hình vuông với diện tích là S 1 ; S 3 ; . . . ; S n ; . . . Tính tổng vô hạn S 1 + S 2 + S 3 + . . . + S n + . . .
A. 1
B. 1/2
C. 2
D. 3/2
Cho hình phẳng (H) giới hạn bởi các đường y = - x 2 + 5 x - 4 và trục hoành. Đường thẳng x=2 chia (H) thành hai hình phẳng ( H 1 ) ; H 2 có diện tích lần lượt là S 1 , S 2 , S 1 < S 2 . Khi đó tỉ số S 1 S 2 là
A. 7/6
B. 10/3
C. 10/7
D. 20/7
Cho hình phẳng giới hạn bởi hai đồ thị hàm số y = log 2 x , x = 4 . Đường thẳng x=2 chia hình phẳng đó thành hai hình có diện tích là S 1 > S 2 . Tỉ lệ diện tích S 1 - 2 S 2 là:
A. 2
B. 7/4
C. 3
D. Đáp án khác
Cho parabol P 1 : y = - x 2 + 2 x + 3 cắt trục hoành tại hai điểm A, B và đường thẳng d : y = a 0 < a < 4 . Xét parabol P 2 đi qua A, B và có đỉnh thuộc đường thẳng y = a . Gọi S 1 là diện tích hình phẳng giới hạn bởi P 1 và d. S 2 là diện tích hình phẳng giới hạn bởi P 2 và trục hoành. Biết S 1 = S 2 , tính T = a 3 - 8 a 2 + 48 a .
A. T = 99
B. T = 64
C. T = 32
D. T = 72
Chọn đáp án B
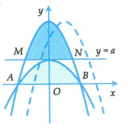
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương trình các parabol mới là
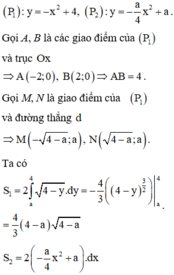
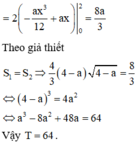
Cho hình phẳng giới hạn bởi hai đồ thị hàm số y = log 2 x ; y = 0 ; x = 4 Đường thẳng x= 2 chia hình phẳng đó thành hai hình có diện tích là S 1 > S 2 Tỉ lệ diện tích S 1 - 1 S 2 là:
A. 2.
B. 7/4
C. 3.
D. Đáp án khác