Các câu hỏi tương tự
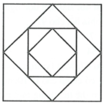
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3,…và cứ thế tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100 (tham khảo hình bên). Tính tổng S S1 + S2 + S3 + … + S100 A.
S
a
2...
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3,…và cứ thế tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100 (tham khảo hình bên). Tính tổng S = S1 + S2 + S3 + … + S100
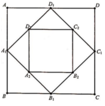
A. S = a 2 2 100 - 1 2 100
B. S = a 2 2 100 - 1 2 99
C. S = a 2 2 100
D. S = a 2 2 99 - 1 2 98
Cho hình vuông ABCD có cạnh bằng a và có diện tích
S
1
.
Nối 4 trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích
S
2
.
Tiếp tục làm như thế ta được hình vuông thứ...
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng a và có diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S 2 . Tiếp tục làm như thế ta được hình vuông thứ ba A 2 B 2 C 2 D 2 có diện tích S 3 …. Và cứ tiếp tục làm như thế ta được các hình vuông có diện tích S 4 , S 5 …, S 100 (tham khảo hình vẽ bên). Tính tổng S = S 1 + S 2 + S 3 + ... + S 100 .
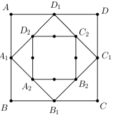
A. S = a 2 2 100 − 1 2 100 .
B. S = a 2 2 100 − 1 2 99 .
C. S = a 2 2 100 .
D. S = a 2 2 99 − 1 2 99 .
Một hình vuông ABCD có cạnh
A
B
a
, diện tích
S
1
. Nối 4 trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai là
A
1
B
1...
Đọc tiếp
Một hình vuông ABCD có cạnh A B = a , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai là A 1 B 1 C 1 D 1 có diện tích S 2 . Tiếp tục như thế ta được hình vuông thứ ba là A 2 B 2 C 2 D 2 có diện tích S 3 và cứ tiếp tục như thế, ta được diện tích S 4 , S 5 , . . .
Tính S = S 1 + S 2 + S 3 + . . . . + S 100

A. S = 2 100 - 1 2 99 a 2
B. S = a 2 100 - 1 2 99
C. S = a 2 2 100 - 1 2 99
D. S = a 2 2 99 - 1 2 99
Một hình vuông
A
B
C
D
có cạnh
A
B
a
.
, diện tích
S
1
.
Nối 4 trung điểm
A
1
,
B
1
,
C
1
,
D
1
theo thứ tự của 4 cạnh
A
B
,
B
C
,...
Đọc tiếp
Một hình vuông A B C D có cạnh A B = a . , diện tích S 1 . Nối 4 trung điểm A 1 , B 1 , C 1 , D 1 theo thứ tự của 4 cạnh A B , B C , C D , D A ta được một hình vuông thứ hai A 1 , B 1 , C 1 , D 1 có diện tích S 2 . Tiếp tục như vậy ta được hình vuông thứ 3 là có diện tích S 3 và cứ như thế ta được S 4 , S 5 ,... Tính giá trị của S = S 1 + S 2 + S 3 + ... + S 100
A. 2 100 − 1 2 99 a 2
B. a 2 100 − 1 2 99
C. a 2 2 100 − 1 2 99
D. a 2 2 99 − 1 2 99
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên). Tổng diện tích cách hình vuông liên tiếp đó là A. 2 B.
3
2
C. 8 D. 4
Đọc tiếp
Cho một hình vuông có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp để được một hình vuông, tiếp tục làm như thế đối với hình vuông mới (như hình vẽ bên).
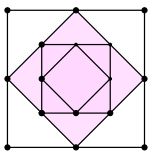
Tổng diện tích cách hình vuông liên tiếp đó là
A. 2
B. 3 2
C. 8
D. 4
Cho hình vuông
C
1
có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông
C
2
(hình vẽ). Từ hình vuông
C
2
lại tiếp tục làm như trên ta nhận được dãy các hình vuông
C
1
,
C
2
,
.
.
.
C...
Đọc tiếp
Cho hình vuông C 1 có cạnh bằng a. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C 2 (hình vẽ). Từ hình vuông C 2 lại tiếp tục làm như trên ta nhận được dãy các hình vuông C 1 , C 2 , . . . C n . Gọi S i là diện tích của hình vuông C i ( i ∈ 1 , 2 , 3 . . . ) . Đặt T = S 1 + S 2 + . . . + S n + . . . biết rằng T=32/3, tính a
A. 2
A. 5 2
C. 2
D. 2 2
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là: A.
a
6
3
B.
a
6
2
C.
a...
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là:
A. a 6 3
B. a 6 2
C. a 6 4
D. a 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng
A
B
a
,
A
C
a
3
, đường thẳng SA tạo với đáy một góc
60
°
. Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi
S
x
q
là diện tích...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng A B = a , A C = a 3 , đường thẳng SA tạo với đáy một góc 60 ° . Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi S x q là diện tích xung quanh của hình nón. Tính S x q
A. S x q = 4 πa 2 3 3
B. S x q = 4 πa 2
C. S x q = 2 πa 2 3 3
D. S x q = 2 πa 2
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B trung điểm của đoạn thẳng DE. Thể tích của khối đa diện ABCDSEF bằng. A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B trung điểm của đoạn thẳng DE. Thể tích của khối đa diện ABCDSEF bằng.
A. 7 6
B. 11 12
C. 2 3
D. 5 6