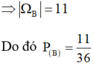Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố A:" Mặt 3 chấm xuất hiện đúng một lần"

Những câu hỏi liên quan
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố B: “ Mặt 3 chấm xuất hiện đúng một lần” A.
P
(
A
)
5
324
B.
P
(
A
)
5
32
C.
P
(
A
)
3
−
5
6
4
D.
P...
Đọc tiếp
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố B: “ Mặt 3 chấm xuất hiện đúng một lần”
A. P ( A ) = 5 324
B. P ( A ) = 5 32
C. P ( A ) = 3 − 5 6 4
D. P ( A ) = 2 − 5 6 4
Gọi B i là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i =1;2; 3; 4
Khi đó: B i ¯ là biến cố “ Mặt 3 chấm không xuất hiện lần thứ i”
Ta có: A = B 1 ¯ . B 2 . B 3 . B 4 ∪ B 1 . B 2 ¯ . B 3 . B 4 ∪ B 1 . B 2 . B 3 ¯ . B 4 ∪ B 1 . B 2 . B 3 . B 4 ¯
Suy ra :
P A = P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4
Mà : P ( B i ) = 1 6 ⇒ P ( B i ¯ ) = 1 − 1 6 = 5 6 .
Do đó: P ( A ) = 4. 1 6 3 . 5 6 = 5 324 .
Chọn đáp án A
Đúng 0
Bình luận (0)
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cốA: “ Mặt 4 chấm xuất hiện ít nhất một lần” A.
P
(
A
)
1
−
5
6
4
B.
P
(
A
)
1
−
1
6
4
C.
P
(
A...
Đọc tiếp
Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố
A: “ Mặt 4 chấm xuất hiện ít nhất một lần”
A. P ( A ) = 1 − 5 6 4
B. P ( A ) = 1 − 1 6 4
C. P ( A ) = 3 − 5 6 4
D. P ( A ) = 2 − 5 6 4
Gọi A i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó: A i là biến cố “ Mặt 4 chấm không xuất hiện lần thứ i”
Và P ( A i ¯ ) = 1 − P ( A i ) = 1 − 1 6 = 5 6
Ta có: A ¯ là biến cố: “ không có mặt 4 chấm xuất hiện trong 4 lần gieo”
Và A ¯ = A 1 ¯ . A 2 ¯ . A 3 ¯ . A 4 ¯ . Vì các A i ¯ độc lập với nhau nên ta có:
P ( A ¯ ) = P ( A 1 ¯ ) . P ( A 2 ¯ ) . P ( A 3 ¯ ) . P ( A 4 ¯ ) = 5 6 4
Vậy P ( A ) = 1 − P ( A ¯ ) = 1 − 5 6 4 .
Chọn đáp án A.
Đúng 0
Bình luận (0)
Gieo ngẫu nhiên xuất sắc một lần. tính xác suất của biến cố :
a ) mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 1
b ) mặt xuất hiện của xúc xắc có số chấm là số lớn hơn 2
a: \(\Omega=\left\{1;2;3;4;5;6\right\}\)
=>n(omega)=6
A={1;4}
=>n(A)=2
=>P(A)=2/6=1/3
b: B={3;4;5;6}
=>n(B)=4
=>P(B)=4/6=2/3
Đúng 1
Bình luận (0)
Gieo một con áuc sắc đồng chất 2 lần . Tính xác suất của biến cố sau
a, trong cả hai lần gieo đều xuất hiện số nguyên tố
b, lần gieo thứ nhất xuất hiện mặt 6 chấm
c, ít nhất 1 lần xuất hiện một mặt 6 chấm
d, không lần nào xuất hiện mặt 6 chấm
Xem chi tiết
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
Đúng 0
Bình luận (0)
Gieo hai con xúc sắc được chế tạo cân đối. Gọi B là biến cố “Có ít nhất một con xúc sắc xuất hiện mặt 1 chấm”. Tính xác suất của biến cố B A. B. C. 1 D.
Đọc tiếp
Gieo hai con xúc sắc được chế tạo cân đối. Gọi B là biến cố “Có ít nhất một con xúc sắc xuất hiện mặt 1 chấm”. Tính xác suất của biến cố B
A. ![]()
B. ![]()
C. 1
D. ![]()
Gieo ngẫu nhiên 1 con xúc xắc cân đối đồng chất 2 lần. Tìm xác suất của biến cố: a) Lần thứ nhất xuất hiện mặt 3 chấm? b) Ít nhất 1 lần xuất hiện mặt 2 chấm? c) Tổng số chấm của 2 lần không lớn hơn 5?
Không gian mẫu: \(6.6=36\)
a.
Lần thứ nhất có 1 khả năng thỏa mãn (3 chấm)
Lần thứ 2 bất kì => có 6 khả năng
\(\Rightarrow1.6=6\) khả năng để lần thứ nhất xuất hiện mặt 3 chấm
Xác suất: \(P=\dfrac{6}{36}=\dfrac{1}{6}\)
b.
Xác suất để cả 2 lần đều ko xuất hiện mặt 2 chấm là: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất để ít nhất 1 lần xuất hiện mặt 2 chấm: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
c.
Các trường hợp có số chấm thuận lợi: (1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(3;1);(3;2);(4;1) có 10 trường hợp
Xác suất: \(P=\dfrac{10}{36}=\dfrac{5}{18}\)
Đúng 0
Bình luận (2)
Câu 1:gieo một đồng xu cân đối và đồng chất 2 lầnXác suất của biến cố2 lần gieo xuất hiện mặt khác nhau làA.1 B.1/4 C.3/4 D.1/2Câu 2:Gieo 1 con xúc sắc cân đối và đồng chất 1 lần.Xác suất biến cốSố chấm xuất hiện là số nguyên tố làA.1/2 B.2/3 C.2/3 D.1/6
Đọc tiếp
Câu 1:gieo một đồng xu cân đối và đồng chất 2 lần>Xác suất của biến cố''2 lần gieo xuất hiện mặt khác nhau'' là
A.1 B.1/4 C.3/4 D.1/2
Câu 2:Gieo 1 con xúc sắc cân đối và đồng chất 1 lần.Xác suất biến cố''Số chấm xuất hiện là số nguyên tố'' là
A.1/2 B.2/3 C.2/3 D.1/6
Câu 1: Gieo 1 đồng tiền cân đối và đồng chất 2 lần
\(\Rightarrow n\left(\Omega\right)=2^2=4\)
Gọi A là biến cố cả hai lần xuất hiện mặt sấp
\(\Rightarrow A=\left\{SS\right\}\Rightarrow n\left(A\right)=1\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{4}\)
Chọn B
Câu 2: Số phần tử không gian mẫu: \(n\left(\Omega\right)=6\)
Gọi biến cố A: “Số chấm là số nguyên tố xuất hiện”
\(A=\left\{2;3;5\right\}\)
\(\Rightarrow n\left(A\right)=3\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{3}{6}=\dfrac{1}{2}\)
Chọn A
Đúng 0
Bình luận (0)
Gieo ngẫu nhiên một con xúc xắc 1 lần, tình xác suất của mỗi biến cố saua) “Mặt xuất hiện của xúc xắc có số chấm là số nguyên tố”.b) “Măt xuất hiện của xúc xắc có số chấm là số chia 4 dư 1”.
Đọc tiếp
Gieo ngẫu nhiên một con xúc xắc 1 lần, tình xác suất của mỗi biến cố sau
a) “Mặt xuất hiện của xúc xắc có số chấm là số nguyên tố”.
b) “Măt xuất hiện của xúc xắc có số chấm là số chia 4 dư 1”.
a: \(\Omega=\left\{1;2;3;4;5;6\right\}\Leftrightarrow n\left(\Omega\right)=6\)
\(A=\left\{2;5\right\}\)
=>P(A)=2/6=1/3
b: B={1;5}
=>n(B)=2
=>P(B)=2/6=1/3
Đúng 0
Bình luận (0)
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:
a) “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”;
b) “Mặt 1 chấm xuất hiện ít nhất một lần”.
Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = \left\{ {(i,j)|i,j = 1,2,3,4,5,6} \right\}\)trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n(\Omega ) = \;36.\)
a) Gọi A là biến cố “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”.
Các kết quả có lợi cho A là: (4; 6) (5;5) (5;6) (6; 4) (6;5) (6;6). Vậy \(n(A) = \;6.\)
Vậy xác suất của biến cố A là \(P(A) = \;\frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}.\)
b) Gọi B là biến cố “Mặt 1 chấm xuất hiện ít nhất một lần”.
Các kết quả có lợi cho B là: (1; 1) (1 : 2) (1 : 3) (1; 4) (1;5) (1; 6) (2 ; 1) (3;1) (4; 1) (5;1) (6;1). Vậy \(n(B) = \;11.\)
Vậy xác suất của biến cố B là: \(P(B) = \;\frac{{n(B)}}{{n(\Omega )}} = \frac{{11}}{{36}}.\)
Đúng 0
Bình luận (0)