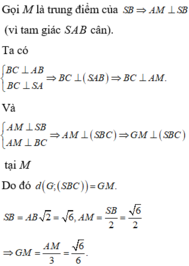cho chóp ∆SABC gọi G,O là trọng tâm ∆SAB,SBC. chứng minh mặt phẳng ABC//GO

Những câu hỏi liên quan
Cho hình chóp Sabc. GỌI h,k là trọng tâm của tam giác SAB, SBC, M là trung điểm của AC. I thuộc SM, SI>IM. Tìm (IHM) và (SBC) Giúp em tìm giao tuyến hai mặt phẳng này vs
Cho hình chóp S ABCD . có đáy ABCD là hình thang với đáy lớn là AB , AB=2CD . Gọi O là giao điểm của AC và BD , G là trọng tâm tam giác SBC .
a. Chứng minh rằng CD // ( SAB )
b. Xác định giao tuyến của hai mặt phẳng ( SAD ) và ( SBD )
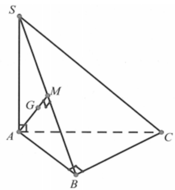
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt đáy và
S
A
A
B
3
. Gọi G là trọng tâm của tam giác SAB. Khoảng cách từ G đến mặt phẳng (SBC) bằng A.
6
3
B.
6
6
C.
3
D.
6...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt đáy và S A = A B = 3 . Gọi G là trọng tâm của tam giác SAB. Khoảng cách từ G đến mặt phẳng (SBC) bằng
A. 6 3
B. 6 6
C. 3
D. 6 2
Cho hình chóp SABC có G là trọng tâm của tam giác ABC. Trên đoạn 5A lấy hai diem M, N sao cho SM = MN = NA
a) Chứng minh: GM // (SBC)
b) Gọi D là điểm đối xứng của A qua G. Chứng minh: (MCD) // (NBG).
c) Gọi H = DM \(\cap\) (SBC). Chứng minh H là trong tâm \(\Delta SBC\)
a) Ta có SM = MN = NA và G là trọng tâm của tam giác ABC. Khi đó, ta có:
SG = 2GM (vì G là trọng tâm)
SG = 2GN (vì G là trọng tâm)
Vậy GM = GN
Do đó, ta có tam giác SMN là tam giác đều.
Vì SM = MN = NA, nên tam giác SNA cũng là tam giác đều.
Từ đó, ta có góc SNA = 60°.
Mà góc SNA = góc SNB + góc BNA = góc SNB + góc BNC.
Vậy góc SNB + góc BNC = 60°.
Nhưng góc SNB + góc BNC = góc SBC.
Vậy góc SBC = 60°.
Do đó, GM // (SBC).
b) Gọi D là điểm đối xứng của A qua G.
Ta có GD = GA (vì D là điểm đối xứng của A qua G)
Và GM = GN (vì G là trọng tâm)
Vậy tam giác GDM và tam giác GAN là tam giác đồng dạng (cạnh bằng nhau và góc bằng nhau).
Từ đó, ta có góc GDM = góc GAN.
Nhưng góc GDM = góc MCD và góc GAN = góc NGB.
Vậy góc MCD = góc NGB.
Do đó, (MCD) // (NBG).
c) Gọi H = DM ∩ (SBC).
Ta cần chứng minh H là trọng tâm của tam giác SBC.
Vì G là trọng tâm của tam giác ABC, nên AG = 2GM.
Và GD = GA (vì D là điểm đối xứng của A qua G).
Từ đó, ta có AD = 2GD.
Vậy D là trọng tâm của tam giác AGD.
Do đó, DH là đường cao của tam giác AGD.
Vậy DH cắt AG tại I sao cho AI = 2IG.
Mà AI = 2IG nên I là trọng tâm của tam giác AGD.
Vậy I nằm trên đường thẳng DM.
Từ đó, ta có H = DM ∩ (SBC) là trọng tâm của tam giác SBC.
Vậy H là trọng tâm của tam giác SBC.
Đúng 1
Bình luận (0)
Cho hình chóp SABC có SA vuông với đáy. SA=2a, tam giác ABC đều có cạnh bằng 4a. Mà M là trung điểm BC
a) CMR: BC vuông với (SAM)
b) Tính d(A;(SBC))
c) Gọi G là trọng tâm tam giác SAB. Tính d(G;(SBC))
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: Kẻ AK vuông góc SM
=>AK=d(A;(SBC))
AM=4a*căn 3/2=2a*căn 3
=>SM=4a
=>AK=2a*2a*căn 3/4a=a*căn 3
Đúng 0
Bình luận (0)
Bài 1: Cho hình chóp SABC có M thuộc (SAB), N thuộc (SAC), O thuộc (SBC). Tìm giao tuyến của hai mặt phẳng (MNO) và (ABC)
Bài 2: Cho hình chóp SABC có H là hình chiếu vuông góc của S trên mặt phẳng (ABC). Tìm giao tuyến của (SAH) và (SBC)
Cho hình chóp S.ABC có đấy ABC là tam giác đều cạnh a, SA = SB = SC = 2a. Gọi o là trung điểm AC, G là trọng tâm tam giác ABC a) chứng minh (SGO) vuông góc với (ABC) b) tính góc giữa hai mặt phẳng (SAB) và (ABC) c) tính khoảng cách giữa AB và SC
a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB AC, SA SB SC 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là: A.
6
a
3
3
25
B.
6
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:
A. 6 a 3 3 25
B. 6 a 3 15 25
C. a 3 3 4
D. 4 a 3 3 5 5
Đáp án B
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: ![]()
Đặt AB = x ta tính được: 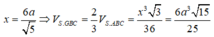
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAB; I và M lần lượt là trung điểm của AB và SD.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD)
b) Gọi N là giao điểm DI và AC. Chứng minh rằng NG song song với (SCD)
c)Tìm giao điểm E của SO và (CGM). Tính tỉ số \(\frac{SE}{SO}\)
Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v


Đúng 1
Bình luận (1)