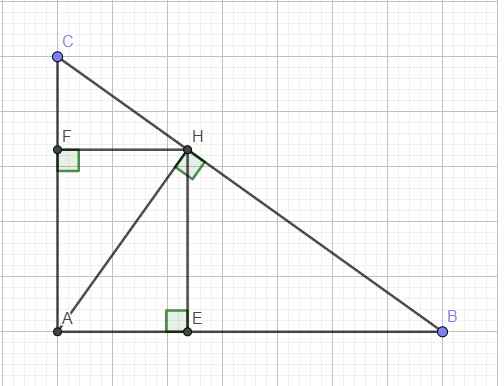
Cho tan giác ABC vuông tại A, đường cao AH. Gọi E,F lần lượt là hình chiếu của H trên AB,AC
Chứng minh rằng BC=AB.cosB+AC.cosC
Help me plsss

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Biết HC = 4cm , HB = 3cm
a) Tính AB , AH
b) Gọi D và E lần lượt là hình chiếu của H trên AB , AC
Chứng minh AD.DB + AE.EC = AH\(^2\)
c) Đường thẳng vuông góc với DE tại E cắt BC tại K.
Chứng minh K là trung điểm của CH
Cho tam giác ABC vuông tại A, đường cao AH. Biết HC = 4cm , HB = 3cm
a) Tính AB , AH
b) Gọi D và E lần lượt là hình chiếu của H trên AB , AC
Chứng minh AD.DB + AE.EC = AH\(^2\)
c) Đường thẳng vuông góc với DE tại E cắt BC tại K.
Chứng minh K là trung điểm của CH
Cho tam giác ABC vuông tại A, đường cao AH. Biết HC = 4cm , HB = 3cm
a) Tính AB , AH
b) Gọi D và E lần lượt là hình chiếu của H trên AB , AC
Chứng minh AD.DB + AE.EC = AH22
c) Đường thẳng vuông góc với DE tại E cắt BC tại K.
Chứng minh K là trung điểm của CH
Cho tam giác ABC vuông tại A , đường cao AH. Gọi E,F lần lượt là hình chiếu của H trên cạnh AB và AC.
a) Chứng minh rằng: AE.AB=AF.AC
b) Chứng minh rằng nếu diện tích tan giác ABC bằng 2 lần diện tích tứ giác AEHF thì tam giác ABC vuông cân.
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và ACa) Chứng minh rằng ΔAEF ΔACBb) Cho AH 4,8cm, BC 10 cm. Tính SAEF?c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC
a) Chứng minh rằng ΔAEF ![]() ΔACB
ΔACB
b) Cho AH = 4,8cm, BC = 10 cm. Tính SAEF?
c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Cho tam giác ABC vuông tại A , đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB,AC Chứng minh AE.EB+ AF.FC= AH^2
Tứ giác AEHF là hình chữ nhật (có 3 góc vuông) \(\Rightarrow HE=AF\)
Áp dụng định lý Pitago trong tam giác vuông AFH:
\(AH^2=AF^2+HF^2=HE^2+HF^2\)
Áp dụng hệ thức lượng trong tam giác vuông AHB với đường cao HF:
\(HF^2=AF.FC\)
Tương tự:
\(HE^2=AE.EB\)
\(\Rightarrow AH^2=HE^2+HF^2=AE.EB+AF.FC\) (đpcm)
Đúng 0
Bình luận (0)
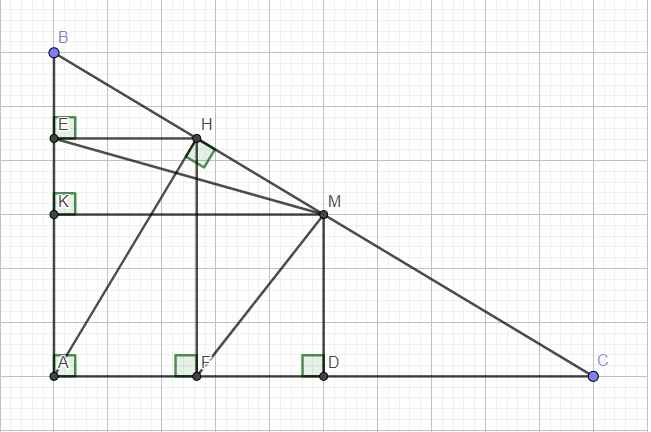
Cho tam giác ABC vuông tại A, đường cao AH. E, F lần lượt là hình chiếu của H trên AB, AC. Gọi M là trung điểm BC. Chứng minh \(S_{AEMF}=\dfrac{1}{2}S_{ABC}\)
Cái bài này thì có lẽ bạn nên chứng minh AM⊥FE là nó ra liền à
Đúng 1
Bình luận (0)
Tứ giác AEHF là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AF\) và \(AE=HF\)
\(S_{ABC}=S_{ABH}+S_{ACH}=\dfrac{1}{2}HE.AB+\dfrac{1}{2}HF.AC=\dfrac{1}{2}AB.AF+\dfrac{1}{2}AC.AE\)
Gọi K là trung điểm AB \(\Rightarrow MK\) là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MK=\dfrac{1}{2}AC\\MK\perp AB\end{matrix}\right.\)
Gọi D là trung điểm AC \(\Rightarrow MD\) là đtb tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MD=\dfrac{1}{2}AB\\MD\perp AC\end{matrix}\right.\)
\(S_{AEMF}=S_{ABC}-\left(S_{BME}+S_{CMF}\right)=S_{ABC}-\left(\dfrac{1}{2}MK.BE+\dfrac{1}{2}MD.CF\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(\dfrac{1}{2}AC.\left(AB-AE\right)+\dfrac{1}{2}AB.\left(AC-AF\right)\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(AB.AC-\left(\dfrac{1}{2}AC.AE+\dfrac{1}{2}AB.AF\right)\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(2S_{ABC}-S_{ABC}\right)=\dfrac{1}{2}S_{ABC}\) (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH , AB = 3cm , BC = 5cm
a) giải tam giác ABC
b) gọi E , F , lần lượt là hình chiếu H trên cạnh AB và AC
- TÍnh độ dài AH
- Chứng minh EF = AH
Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)
Đúng 1
Bình luận (1)