a: Để hàm số đồng biến thì 2m-6>0

hay m>3

b: Phương trình hoành độ giao điểm là:

\(x^2-\left(2m-6\right)x-m+9=0\)

\(\text{Δ}=\left(2m-6\right)^2-4\left(-m+9\right)\)

\(=4m^2-24m+36+4m-36\)

=4m²-20m

Để (P) tiếp xúc với (d) thì 4m(m-5)=0

=>m=0 hoặc m=5

Phương trình hoành độ giao điểm là:

\(x^2-3x+2=mx+2\)

=>\(x^2-3x+2-mx-2=0\)

=>\(x^2+x\left(-m-3\right)=0\)

\(\Delta=\left(-m-3\right)^2-4\cdot1\cdot1=\left(m+3\right)^2-4=\left(m+3-2\right)\left(m+3+2\right)=\left(m+1\right)\left(m+5\right)\)

Để (P) tiếp xúc với (d) thì Δ=0

=>(m+1)(m+5)=0

=>\(\left[{}\begin{matrix}m+1=0\\m+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-5\end{matrix}\right.\)

a: Khi m=4 thì y=4x-4

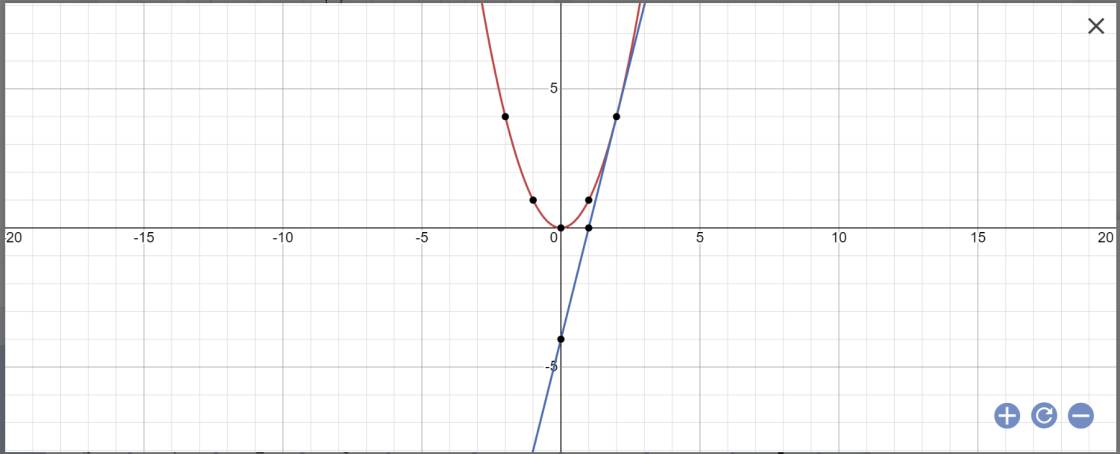
b: PTHDGĐ là:

x^2-mx+4=0

Δ=(-m)^2-4*1*4=m^2-16

Để (P) tiếpxúc với(d) thì m^2-16=0

=>m=4 hoặc m=-4

a) (d) đi qua \(A\left(1;5\right)\Rightarrow5=2m+2m-3\Rightarrow4m=8\Rightarrow m=2\)

\(\Rightarrow y=4x+1\)

b) pt hoành độ giao điểm \(x^2-2mx-2m+3=0\)

Để (d) tiếp xúc với (P) thì pt có nghiệm kép \(\Delta=0\)

\(\Delta=\left(2m\right)^2+8m-12=4m^2+8m-12\)

\(\Rightarrow4m^2+8m-12=0\Rightarrow m^2+2m-3=0\Rightarrow\left(m-1\right)\left(m+3\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)

Xét pt hoành độ gđ của (P) và (d) có:

\(2x^2=mx+1\)

\(\Leftrightarrow2x^2-mx-1=0\) (1)

Để (P) và (d) tiếp xúc <=> Pt (1) có nghiệm kép <=>\(\Delta=0\)<=> \(m^2-4.2\left(-1\right)=0\) <=> \(m^2+8=0\) (vô nghiệm)

Vậy không tồn tại m để (d) và (P) tiếp xúc

Lời giải:

Để $(d)$ đi qua $A(-1;-2)$ thì: $-2=-m+n(1)$

Để $(d)$ và $(P)$ tiếp xúc nhau thì PT hoành độ giao điểm:

$\frac{1}{4}x^2-mx-n=0$ có nghiệm duy nhất

Điều này xảy ra khi:

$\Delta=m^2+n=0(2)$

Từ $(1);(2)\Rightarrow m=1$ hoặc $m=-2$

Nếu $m=1$ thì $n=-1$

Nếu $m=-2$ thì $n=-4$

Vậy............