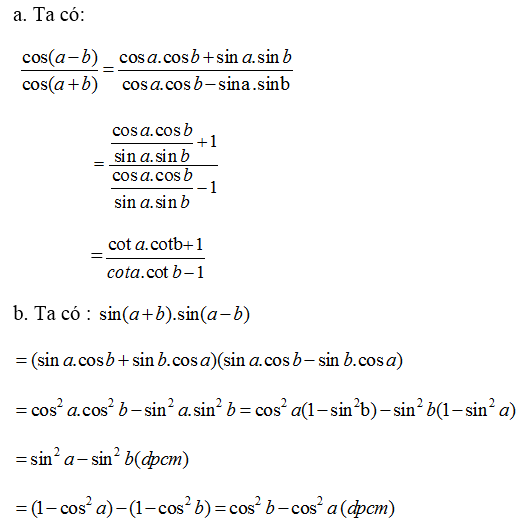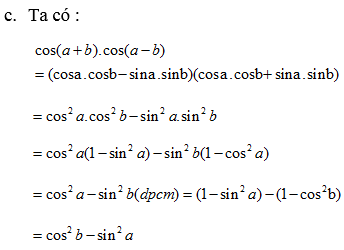\(\dfrac{\sin^2a-\tan^2a}{\cos^2a-\cot^2a}=\dfrac{\sin^2a-\dfrac{\sin^2a}{\cos^2a}}{\cos^2a-\dfrac{\cos^2a}{\sin^2a}}=\dfrac{\dfrac{\sin^2a\cos^2a-\sin^2a}{\cos^2a}}{\dfrac{\cos^2a\sin^2a-\cos^2a}{\sin^2a}}=\dfrac{\sin^2a\sin^2a\left(\cos^2a-1\right)}{\cos^2a\cos^2a\left(\sin^2a-1\right)}\)

\(=\dfrac{\sin^4a\left(\cos^2a-\cos^2a-\sin^2a\right)}{\cos^4a\left(\sin^2a-\cos^2a-\sin^2a\right)}=\dfrac{\sin^4a\left(-\sin^2a\right)}{\cos^4a\left(-\cos^2a\right)}\)

\(=\dfrac{-\sin^6a}{-\cos^6a}=\dfrac{\sin^6a}{\cos^6a}=\tan^6a\)

Lời giải:

a)

\(\frac{\sin ^2a+2\cos ^2a-1}{\cot ^2a}=\frac{(\sin ^2a+\cos ^2a)+\cos ^2a-1}{\cot ^2a}=\frac{1+\cos ^2a-1}{\cot ^2a}=\frac{\cos ^2a}{\cot ^2a}=\frac{\cos ^2a}{(\frac{\cos a}{\sin a})^2}=\sin ^2a\)

b)

\(\frac{1-\sin ^2a\cos ^2a}{\cos ^2a}-\cos ^2a=\frac{1}{\cos ^2a}-\sin ^2a-\cos ^2a\)

\(=\frac{\sin ^2a+\cos ^2a}{\cos ^2a}-(\sin ^2a+\cos ^2a)=\tan ^2a+1-1=\tan ^2a\)

c)

\(\frac{\sin ^2a-\tan ^2a}{\cos ^2a-\cot ^2a}=\frac{\sin ^2a-\frac{\sin ^2a}{\cos ^2a}}{\cos ^2a-\frac{\cos ^2a}{\sin ^2a}}=\frac{\sin ^4a(\cos ^2a-1)}{\cos ^4a(\sin ^2a-1)}\)

\(=\frac{\sin ^4a(-\sin ^2a)}{\cos ^4a(-\cos ^2a)}=\frac{\sin ^6a}{\cos ^6a}=\tan ^6a\)

a.

\(tana=\dfrac{sina}{cosa}=\dfrac{1}{15}\Rightarrow sina=\dfrac{cosa}{15}\)

\(\Rightarrow sin2a=2sina.cosa=\dfrac{2cosa}{15}.cosa=\dfrac{2}{15}cos^2a=\dfrac{2}{15}.\dfrac{1}{1+tan^2a}=\dfrac{2}{15}.\dfrac{1}{1+\dfrac{1}{15^2}}=\dfrac{15}{113}\)

b.

\(5^2=\left(3sina+4cosa\right)^2\le\left(3^2+4^2\right)\left(sin^2+cos^2a\right)=25\)

Đẳng thức xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}\dfrac{sina}{3}=\dfrac{cosa}{4}\\3sina+4cosa=5\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}sina=\dfrac{3}{5}\\cosa=\dfrac{4}{5}\end{matrix}\right.\)

c.

\(\dfrac{1}{tan^2a}+\dfrac{1}{cot^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)

\(\Leftrightarrow\dfrac{cos^2a}{sin^2a}+\dfrac{sin^2a}{cos^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)

\(\)\(\Leftrightarrow\dfrac{sin^4a+cos^4a}{sin^2a.cos^2a}+\dfrac{sin^2a+cos^2a}{sin^2a.cos^2a}=7\)

\(\Leftrightarrow\dfrac{\left(sin^2a+cos^2a\right)^2-2sin^2a.cos^2a}{sin^2a.cos^2a}+\dfrac{1}{sin^2a.cos^2a}=7\)

\(\Leftrightarrow\dfrac{2}{sin^2a.cos^2a}=9\)

\(\Leftrightarrow\dfrac{8}{\left(2sina.cosa\right)^2}=9\)

\(\Leftrightarrow\dfrac{8}{sin^22a}=9\)

\(\Leftrightarrow sin^22a=\dfrac{8}{9}\)

\(\frac{cosa}{1+sina}+\frac{sina}{cosa}=\frac{cos^2a+sina\left(1+sina\right)}{cosa\left(1+sina\right)}=\frac{1+sina}{cosa\left(1+sina\right)}=\frac{1}{cosa}\)

\(\frac{sin^2a+cos^2a+2sina.cosa}{\left(sina-cosa\right)\left(sina+cosa\right)}=\frac{\left(sina+cosa\right)^2}{\left(sina-cosa\right)\left(sina+cosa\right)}=\frac{sina+cosa}{sina-cosa}=\frac{\frac{sina}{cosa}+1}{\frac{sina}{cosa}-1}=\frac{tana+1}{tana-1}\)

\(\left(sin^2a\right)^3+\left(cos^2a\right)^3=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\)

\(=1-3sin^2a.cos^2a\)

\(sin^2a-tan^2a=tan^4a\left(\frac{sin^2a}{tan^4a}-\frac{1}{tan^2a}\right)=tan^4a\left(sin^2a.\frac{cos^2a}{sin^2a}-\frac{1}{tan^2a}\right)\)

\(=tan^4a\left(cos^2a-cot^2a\right)\) bạn ghi sai đề câu này

\(\frac{tan^3a}{sin^2a}-\frac{1}{sina.cosa}+\frac{cot^3a}{cos^2a}=tan^3a\left(1+cot^2a\right)-\frac{1}{sina.cosa}+cot^3a\left(1+tan^2a\right)\)

\(=tan^3a+tana-\frac{1}{sina.cosa}+cot^3a+cota\)

\(=tan^3a+cot^3a+\frac{sina}{cosa}+\frac{cosa}{sina}-\frac{1}{sina.cosa}\)

\(=tan^3a+cot^3a+\frac{sin^2a+cos^2a-1}{sina.cosa}=tan^3a+cot^3a\)

\(\dfrac{1}{tan^2a}+\dfrac{1}{cot^2a}+\dfrac{1}{sin^2a}+\dfrac{1}{cos^2a}=7\)

=>\(\dfrac{sin^2a+1}{cos^2a}+\dfrac{cos^2a+1}{sin^2a}=7\)

=>\(\dfrac{sin^4a+sin^2a+cos^4a+cos^2a}{sin^2a\cdot cos^2a}=7\)

=>\(sin^4a+cos^4a+1=7\cdot sin^2a\cdot cos^2a\)

=>\(\left(sin^2a+cos^2a\right)^2-2\cdot sin^2a\cdot cos^2a+1=7\cdot sin^2a\cdot cos^2a\)

=>\(2=9\cdot sin^2a\cdot cos^2a\)

=>\(8=9\cdot sin^22a\)

=>16=9(1-cos4a)

=>1-cos4a=16/9

=>cos4a=-7/9

\(VT=\dfrac{sin^23a.cos^2a-sin^2a.cos^23a}{\left(sina.cosa\right)^2}\)

\(=\dfrac{\left(sin3a.cosa-sina.cos3a\right)\left(sin3a.cosa+sina.cos3a\right)}{\dfrac{1}{4}sin^22a}\)

\(=\dfrac{4sin2a.sin4a}{sin^22a}=\dfrac{4sin4a}{sin2a}=\dfrac{8.sin2a.cos2a}{sin2a}=8cos2a\)