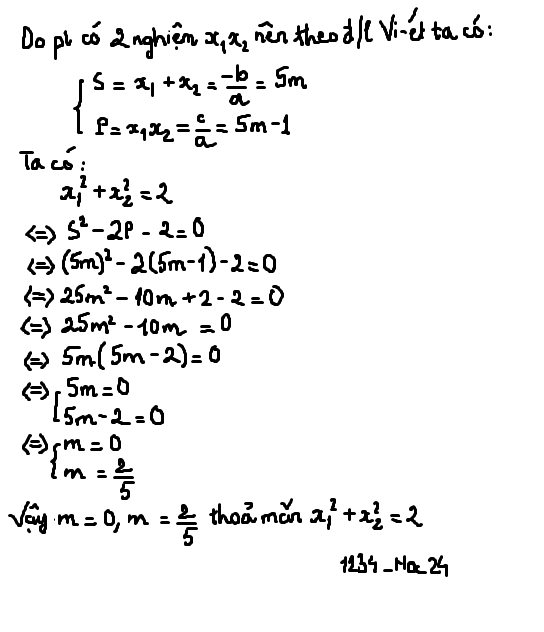\(\text{∆}=\left(-5m\right)^2-4.\left(5m-1\right)\)

\(=25m^2-20m+4\)

\(=\left(5m-2\right)^2>0\forall m\)

Do phương trình có 2 nghiệm x₁, x₂

_{\(\Rightarrow\left\{{}\begin{matrix}S=x_1+x_2=5m\\P=x_1.x_2=5m-1\end{matrix}\right.\)}

Ta có: 

\(x_1^2+x_2^2=2\)

\(\left(x_1^2+2x_1x_2+x_2^2\right)-2x_1x_2=2\)

\(\left(x_1+x_2\right)^2-2x_1x_2-2=0\)

\(\left(5m^2\right)-2\left(5m-1\right)-2=0\)

\(25m^2-10m+2-2=0\)

\(25m^2-10m=0\)

\(5m\left(5m-2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{2}{5}\end{matrix}\right.\)

Vậy ...

Do pt có 2 nghiệm phân biệt \(x_1,x_2\) nên theo đ/l Vi-ét , ta có :

\(\left\{{}\begin{matrix}S=x_1+x_2=-\dfrac{b}{a}=3m\\P=x_1x_2=\dfrac{c}{a}=3m-1\end{matrix}\right.\)

Ta có :

\(x_1^2+x_2^2=6\)

\(\Leftrightarrow S^2+2P-6=0\)

\(\Leftrightarrow\left(3m\right)^2+2\left(3m-1\right)-6=0\)

\(\Leftrightarrow9m^2+6m-2-6=0\)

\(\Leftrightarrow9m^2+6m-8=0\)

\(\Delta=b^2-4ac=6^2-4.9.\left(-8\right)=324>0\)

\(\Rightarrow\)Pt có 2 nghiệm \(m_1,m_2\)

\(\left\{{}\begin{matrix}m_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-6+18}{18}=\dfrac{2}{3}\\m_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-6-18}{18}=-\dfrac{4}{3}\end{matrix}\right.\)

Vậy \(m=\dfrac{2}{3};m=-\dfrac{4}{3}\) thì thỏa mãn \(x_1^2+x_2^2=6\)

\(\Delta=\left(-3m\right)^2-4\left(3m-1\right)\)

 \(=9m^2-12m+4=\left(3m-1\right)^2+3>0\)

=> pt luôn có 2 nghiệm phân biệt 

Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=3m\\x_1.x_2=3m-1\end{matrix}\right.\)

\(x_1^2+x_2^2=6\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=6\)

\(\Leftrightarrow\left(3m\right)^2-2\left(3m-1\right)=6\)

\(\Leftrightarrow9m^2-6m+2=6\)

\(\Leftrightarrow9m^2-6m-4=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1-\sqrt{5}}{3}\\x=\dfrac{1+\sqrt{5}}{3}\end{matrix}\right.\)

ê phải n.nam 9c ko

x1+x2=2m+2; x1x2=m^2+4

x1^2+2(m+1)x2<=2m^2+20

=>x1^2+x2(x1+x2)<=2m^2+20

=>x1^2+x2x1+x2^2<=2m^2+20

=>(x1+x2)^2-x1x2<=2m^2+20

=>(2m+2)^2-(m^2+4)<=2m^2+20

=>4m^2+8m+4-m^2-4-2m^2-20<=0

=>m^2-8m-20<=0

=>m<=-10 hoặc m>2

\(x^2-2\left(m+1\right)x+m^2+4=0\left(1\right)\)

Để phương trình có hai nghiệm phân biệt thì \(\Delta'>0\) hay \(\Delta'=\left(m+1\right)^2-m^2-4=m^2+2m+1-m^2-4=2m-4>0\Leftrightarrow m>2\)

Theo hệ thức Viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+4\end{matrix}\right.\)

Vì \(x_1^2\) là nghiệm của phương trình (1) nên ta có : \(x_1^2-2\left(m+1\right)x+m^2+4=0\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)

Ta lại có : \(x_1^2+2\left(m+1\right)x_2\le2m^2+20\)

\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le2m^2+20\)

\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-m^2-4\le2m^2+20\)

\(\Leftrightarrow4\left(m+1\right)^2-m^2\le2m^2+20\)

\(\Leftrightarrow4\left(m^2+2m+1\right)-m^2\le2m^2+20\)

\(\Leftrightarrow m^2+8m-16\le0\)

\(\Leftrightarrow-10\le m\le2\)

Kết hợp điều kiện....

\(\Delta=25-4\left(m-3\right)>0\Rightarrow m< \dfrac{37}{4}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-3\end{matrix}\right.\)

Do \(x_1\) là nghiệm của pt nên:

\(x_1^2-5x_1+m-3=0\Leftrightarrow x_1^2-4x_1+m-3=x_1\)

Thay vào bài toán:

\(\sqrt{x_1^2-4x_1+m-3}=3-\sqrt{x_2}\)

\(\Leftrightarrow\sqrt{x_1}=3-\sqrt{x_2}\Leftrightarrow\sqrt{x_1}+\sqrt{x_2}=3\) (1)

Để (1) xác định \(\Rightarrow x_1;x_2\ge0\Rightarrow m\ge3\)

Khi đó bình phương 2 vế của (1) ta được:

\(x_1+x_2+2\sqrt{x_1x_2}=9\)

\(\Leftrightarrow5+2\sqrt{m-3}=9\Rightarrow\sqrt{m-3}=2\Rightarrow m=7\)

\(x^2-\left(m+4\right)x+4m=0\) (1)

a)Thay x=2 vào pt (1) ta được: \(4-\left(m+4\right).2+4m=0\) \(\Leftrightarrow m=2\)

Thay m=2 vào pt (1) ta được: \(x^2-6x+8=0\)\(\Leftrightarrow x^2-4x-2x+8=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-2\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)

Vậy nghiệm còn lại là 4

b)Để pt có hai nghiệm pb \(\Leftrightarrow\Delta>0\Leftrightarrow m^2-8m+16>0\)\(\Leftrightarrow\left(m-4\right)^2>0\)\(\Leftrightarrow m\ne4\)

Do x₁ là một nghiệm của pt \(\Rightarrow x_1^2-\left(m+4\right)x_1+4m=0\)

​\(\Rightarrow x_1^2=\left(m+4\right)x_1-4m=0\)​

Theo viet có: \(x_1+x_2=m+4\)

\(x_1^2+\left(m+4\right)x_2=16\)

\(\Leftrightarrow\left(m+4\right)x_1-4m+\left(m+4\right)x_2=16\)

\(\Leftrightarrow\left(m+4\right)\left(x_1+x_2\right)-4m-16=0\)

\(\Leftrightarrow\left(m+4\right)^2-4m-16=0\)

\(\Leftrightarrow m^2+4m=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-4\end{matrix}\right.\)(Thỏa)

Vậy...