Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón, hình nón cụt
Các câu hỏi tương tự
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (OA OB). Hãy so sánh tổng các thể tích của hai hình nón và thể tích của hình trụ.
R O A B h
Đọc tiếp
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (OA = OB). Hãy so sánh tổng các thể tích của hai hình nón và thể tích của hình trụ.
Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Đọc tiếp
Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Hình ABCD khi quay quanh BC thì tạo ra:
(A) Một hình trụ; (B) Một hình nón; (C) Một hình nón cụt;
(D) Hai hình nón; (E) Hai hình trụ.
Hãy chọn câu trả lời đúng.
A B C D
Đọc tiếp
Hình ABCD khi quay quanh BC thì tạo ra:
(A) Một hình trụ; (B) Một hình nón; (C) Một hình nón cụt;
(D) Hai hình nón; (E) Hai hình trụ.
Hãy chọn câu trả lời đúng.
Hãy điền đủ vào các ô trống ở bảng sau (đơn vị độ dài: cm).
Hình Bán kính đáy Chiều cao Độ dài đường Thể tích 5 7 12 16 40 15 Đường kính đáy sinh 25 29
Đọc tiếp
Hãy điền đủ vào các ô trống ở bảng sau (đơn vị độ dài: cm).
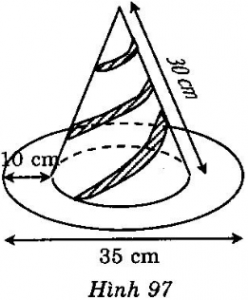
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h. 97). Hãy tính tổng diện tích vải cần có để làm lên cái mũ (không kể riềm, mép, phần thừa).
Hình 101 :
Có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là :
(A) dfrac{k}{4}cm (B) dfrac{k}{3}cm
(C) dfrac{2k}{3}cm (D) dfrac{3k}{4}cm
Hãy chọn kết quả đúng ?
Đọc tiếp
Hình 101 :
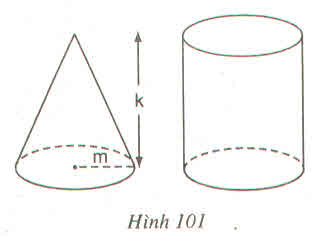
Có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là :
(A) \(\dfrac{k}{4}cm\) (B) \(\dfrac{k}{3}cm\)
(C) \(\dfrac{2k}{3}cm\) (D) \(\dfrac{3k}{4}cm\)
Hãy chọn kết quả đúng ?
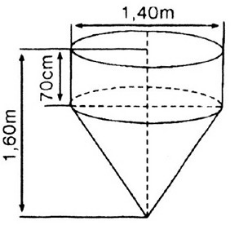
Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình 100. Hãy tính:
a) Thể tích của dụng cụ này;
b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).
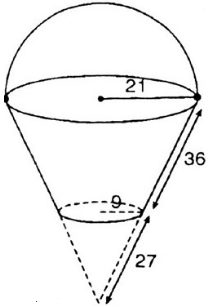
Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị cm).
a) Hãy tính diện tích xung quanh của xô.
b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu?
Chiếc nón do làng Chuông ( Thanh Oai - Hà Nội) sản xuất là hình nón có đường sinh bằng 30cm, đường kính bằng 40cm. Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh nón. Tính diện tích là cần dùng làm một chiếc nón





