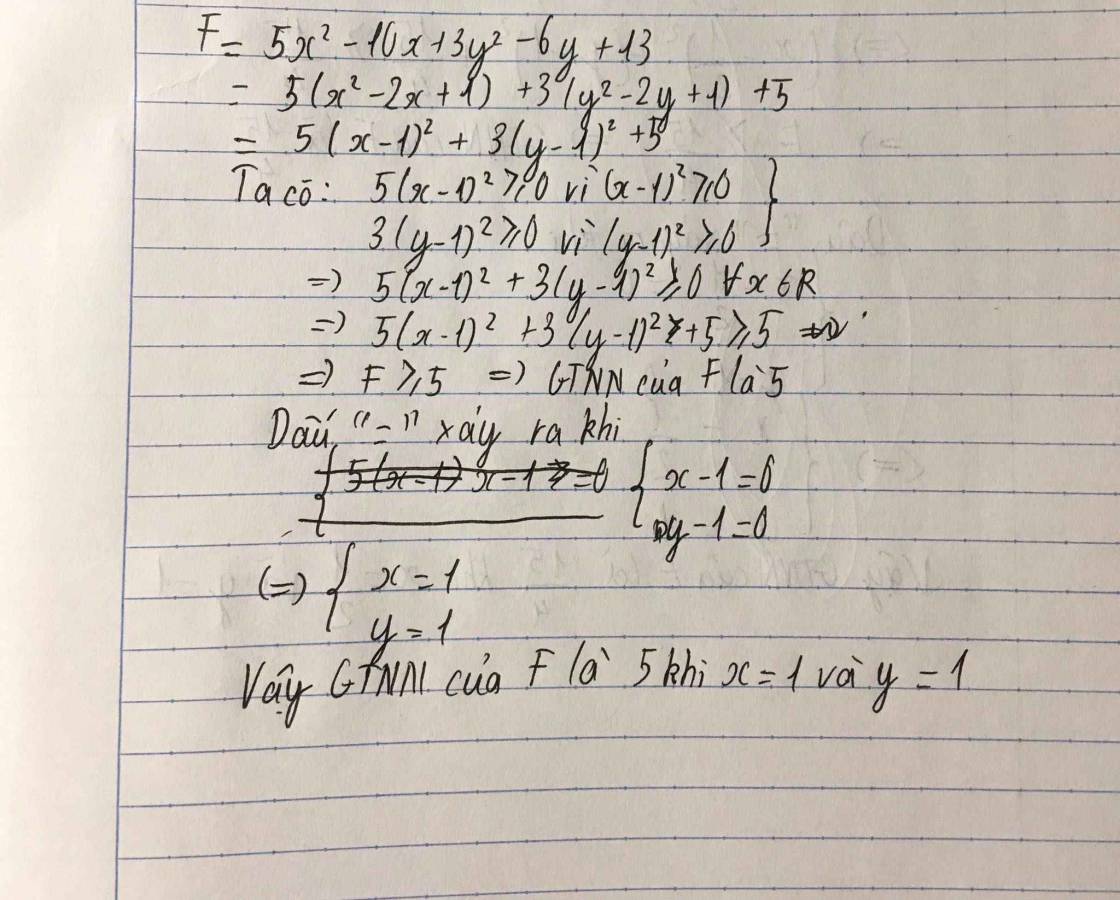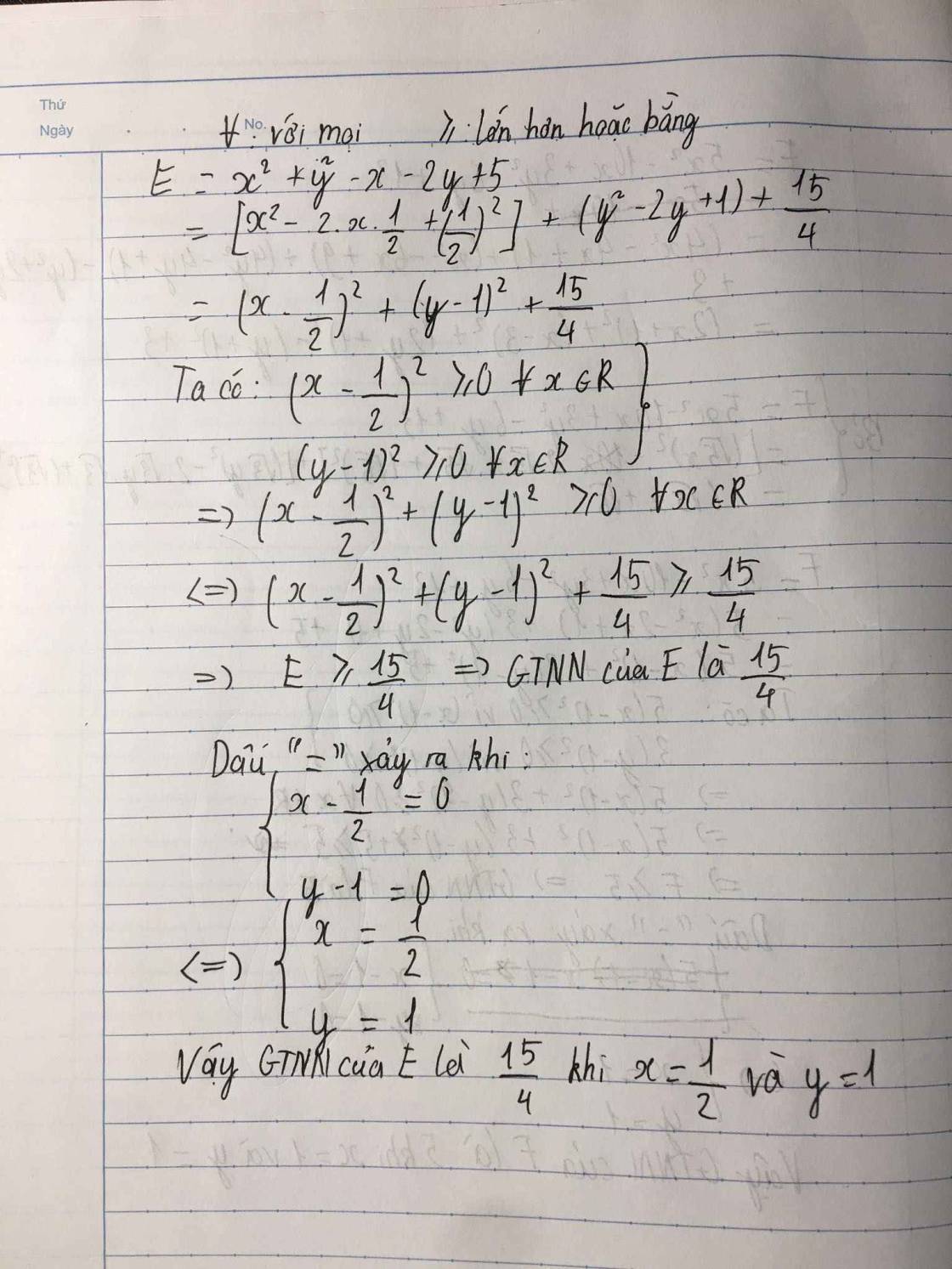Câu 2:

ĐKXĐ: x<>0

\(B=\dfrac{-x^2-x-1}{x^2}\)

\(=-1-\dfrac{1}{x}-\dfrac{1}{x^2}\)

\(=-\left(\dfrac{1}{x^2}+\dfrac{1}{x}+1\right)\)

\(=-\left(\dfrac{1}{x^2}+2\cdot\dfrac{1}{x}\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)\)

\(=-\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< =-\dfrac{3}{4}\forall x< >0\)

Dấu '=' xảy ra khi 1/x+1/2=0

=>1/x=-1/2

=>x=-2

a: Ta có: \(A=2x^2-8x+1\)

\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)

\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)

\(=2\left(x-2\right)^2-7\ge-7\forall x\)

Dấu '=' xảy ra khi x=2

bạn làm rõ ra dc ko mik ko hiểu

A=5x2+2y2−4xy−8x−4y+19=(2x2−4xy+2y2)+4(x−y)+(3x2−12x)+19=2(x−y)2+4(x−y)+3(x2−4x+4)+7=2[(x−y)2+2(x−y)+1]+3(x−2)2+5=2(x−y+1)2+3(x−2)2+5≥0Dấu "=" xảy ra khi{x−y+1=0x−2=0↔{x=2y=x+1=3VậyMinA=5↔{x=2y=3

mik viết 5x2 là 5x mũ 2 nha

Ta có: \(\left(x-1\right)^2\ge0\forall x=>-\left(x-1\right)^2\le0\forall x=>B=8-\left(x-1\right)^2\le8\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x-1=0\Leftrightarrow x=1\)

Vậy MinB = 8 khi và chỉ khi x=1

Ta có: \(2\left(x-1\right)^2+3\ge3\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x=1\)

\(\Rightarrow B=\dfrac{1}{2\left(x-1\right)^2+3}\le\dfrac{1}{3}\)

Dấu "=" xảy ra \(\Leftrightarrow x=1\)

Vậy \(B_{max}=\dfrac{1}{3}\Leftrightarrow x=1\)

Ta có: \(B=-x^2-2x+2\)

\(\Rightarrow BMax\Leftrightarrow-x^2-2x+2Max\)

\(\Leftrightarrow-\left(x^2+2x-2\right)Max\)

\(\Leftrightarrow-\left(x^2+2x+1-3\right)Max\)

\(\Leftrightarrow-\left[\left(x+1\right)^2-3\right]Max\)

\(\Leftrightarrow-\left(x+1\right)^2+3Max\)

Vì \(-\left(x+1\right)^2\le0\forall x\)

\(\Rightarrow-\left(x+1\right)^2+3\le3\forall x\)

Dấu = xảy ra \(\Leftrightarrow x+1=0\)

\(\Leftrightarrow x=-1\)

\(\Rightarrow MaxB=3\Leftrightarrow x=-1\)

Với \(x\ge\dfrac{1}{3}\Leftrightarrow B=9x^2-6x-4\left(3x-1\right)+6=9x^2-18x+10\)

\(B=9\left(x^2-2x+1\right)+1=9\left(x-1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=1\left(1\right)\)

Với \(x< \dfrac{1}{3}\Leftrightarrow B=9x^2-6x+4\left(3x-1\right)+6=9x^2+6x+2\)

\(B=\left(9x^2+6x+1\right)+1=\left(3x+1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=-\dfrac{1}{3}\left(2\right)\)

\(\left(1\right)\left(2\right)\Leftrightarrow B_{min}=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

\(C=2x^2+4x+2+3x^2+12x+12-4x^2-24x-36\\ C=x^2-8x-22=\left(x^2-8x+16\right)-38=\left(x-4\right)^2-38\ge-38\\ C_{min}=-38\Leftrightarrow x=4\)

Với \(x\ge\dfrac{1}{6}\Leftrightarrow A=5x^2-6x+1-1=5x^2-6x\)

\(A=5\left(x^2-2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{9}{5}=5\left(x-\dfrac{3}{5}\right)^2-\dfrac{9}{5}\ge-\dfrac{9}{5}\\ A_{min}=-\dfrac{9}{5}\Leftrightarrow x=\dfrac{3}{5}\left(1\right)\)

Với \(x< \dfrac{1}{6}\Leftrightarrow A=5x^2+6x-1-1=5x^2+6x-2\)

\(A=5\left(x^2+2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{19}{5}=5\left(x+\dfrac{3}{5}\right)^2-\dfrac{19}{5}\ge-\dfrac{19}{5}\\ A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\)