Để hai tam giác ABC và EDF đồng dạng thì số đo góc D trong hình vẽ
dưới bằng:
Để hai tam giác ABC và EDF đồng dạng thì số đo góc D trong hình vẽ dưới bằng:
A. 50 ∘
B. 60 ∘
C. 30 ∘
D. 70 ∘
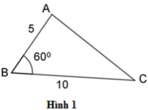
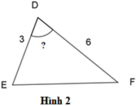
Có: B A B C = 5 10 = 1 2 , D E D F = 3 6 = 1 2
Để hai tam giác đã cho đồng dạng thì góc ABC = EDF = 60 ∘ .
Đáp án: B
hãy thêm điều kiện đề tam giác ABC và tam giác EDF đồng dạng theo trường hợp góc cạnh góc.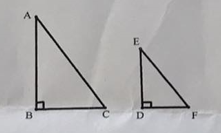
Cho tam giác ABC nhọn. Điểm M trong tam giác sao cho hiệu số đo góc AMB và ACB bằng hiệu số đo góc AMC và góc ABC. Dựng tam giác AMN đồng dạng với tam giác ACB sao cho điểm N thuộc nửa mặt phẳng bờ là đường thẳng AB không chưa đỉnh C.
CMR:
a) Tam giác ANB đồng dạng với tam giác AMC. từ đó suy ra tam giác BMN cân.
b) MB : MC = AB : AC
Cho tam giác ABC nhọn ( AB < AC ) có hai đường cao BE, CF cắt nhau tại H.
Gọi D là giao điểm của AH và BC.
Chứng minh tam giác AEB đồng dạng tam giác AFC và AH. CD = HE. AC
Chứng minh DA là phân giác của góc EDF
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Bài 1: Lấy điểm M và N trên hai cạnh AB và BC của tam giác đều ABC sao cho MN//AC. Lấy điểm P trên cạnh AC sao cho góc CNP=60 độ. Chứng minh tứ giác AMNP là hình bình hành.
BÀi 2: Cho tam giác đều ABC. Lấy D thuộc AB, E thuộc AC, F thuộc BC sao cho góc EDF=60độ , và góc DFC=120 độ.
1) Tính số đo góc DEC
2) CHứng minh tứ giác DEFC là hình bình hành
Cho tam giác ABC bằng tam giác DEF (H. 4.13). Biết rằng BC = 4 cm, \(\widehat {ABC} = 40^\circ ;\widehat {ACB} = 60^\circ \). Hãy tính độ dài đoạn thẳng EF và số đo góc EDF.
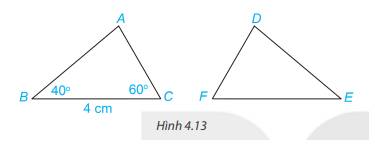
Vì \(\Delta ABC = \Delta DEF\) nên BC = EF ( 2 cạnh tương ứng); \(\widehat A = \widehat {EDF}\) ( 2 góc tương ứng)
Mà BC = 4 cm nên EF = 4 cm
Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 60^\circ = 180^\circ \\ \Rightarrow \widehat A = 180^\circ - 40^\circ - 60^\circ = 80^\circ \end{array}\)
Mà \(\widehat A = \widehat {EDF}\) nên \(\widehat {EDF} = 80^\circ \)
Cho tam giác ABC đồng dạng với tam giác DEF biết góc A=90° tính số đo góc D
Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó
Ba điểm D, E, F theo thứ tự là trung điểm của các cạnh AB, BC và CA. Ba điểm M, P, Q theo thứ tự là trung điểm của các đoạn thẳng OA, OB và OC
a) Các tam giác DEF và MPQ có đồng dạng với nhau không ? Vì sao ? Tỉ số đồng dạng bằng bao nhiêu ?
Hãy sắp xếp các đỉnh tương ứng nếu hai tam giác đó đồng dạng
b) Khi nào thì lục giác DPEQFM có tất cả các cạnh bằng nhau ? Hãy vẽ hình trong trường hợp đó ?
Cho tam giác ABC = tam giác MNP. Biết rằng ,
. Số đo của
là :
Cho và
là hai đại lượng tỉ lệ nghịch với nhau và khi
thì
. Giá trị
khi
bằng
Cho hình vẽ , biết : d MQ, d
NP và
. Số đo x của góc NPQ bằng :
Với x là số hữu tỉ khác 0, tích x6.x2 bằng:
Cho có :
và
, khi đó số đo của góc B là:
Cho hình vẽ. Cần phải có thêm yếu tố nào để ∆ BAC = ∆ DAC ( c- g-c)
Điểm A (1; 3) nằm trên đồ thị của hàm số:
Cứ xay xát 40 kg thóc thì được 32 kg gạo. Hỏi nếu xay xát 150 kg thóc thì được bao nhiêu ki-lô-gam gạo ?
Cho hai tam giác và
có
Cần thêm điều kiện nào dưới đây để hai tam giác
và
bằng nhau theo trường hợp góc - cạnh - góc?
chỉ ghi đáp án thui nha . mik đang cần gấp ![]()