\(a,x-5\left(x-2\right)=6x\\ \Leftrightarrow x-5x+10-6x=0\\ \Leftrightarrow-10x+10=0\\ \Leftrightarrow x=1\\ b,2^3+3x^2-32x=48\\ \Leftrightarrow3x^2-32x+8=48\\ \Leftrightarrow3x^2-32x-40=0\)

Nghiệm xấu lắm bn

\(c,\left(3x+1\right)\left(x-3\right)^2=\left(3x+1\right)\left(2x-5\right)^2\\ \Leftrightarrow c,\left(3x+1\right)\left[\left(2x-5\right)^2-\left(x-3\right)^2\right]\\ \Leftrightarrow\left(3x+1\right)\left(2x-5-x+3\right)\left(2x-5+x-3\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x-2\right)\left(3x-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=2\\x=\dfrac{8}{3}\end{matrix}\right.\)

\(d,9x^2-1=\left(3x+1\right)\left(4x+1\right)\\ \Leftrightarrow\left(3x+1\right)\left(4x+1\right)-\left(3x-1\right)\left(3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(4x+1-3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-2\end{matrix}\right.\)

\(b,2x^3+3x^2-32x-48=0\\ \Leftrightarrow\left(2x^3-8x^2\right)+\left(11x^2-44x\right)+\left(12x-48\right)=0\\ \Leftrightarrow2x^2\left(x-4\right)+11x\left(x-4\right)+12\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(2x^2+11x+12\right)=0\\ \Leftrightarrow\left(x-4\right)\left[\left(2x^2+8x\right)+\left(3x+12\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left[2x\left(x+4\right)+3\left(x+4\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left(2x+3\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{3}{2}\\x=-4\end{matrix}\right.\)

Bài 1 : 

\(\frac{4x-5}{x-1}=\frac{2+x}{x-1}\)ĐK : x \(\ne\)1

\(\Leftrightarrow\frac{4x-5}{x-1}-\frac{2-x}{x-1}=0\Leftrightarrow\frac{4x-5-2+x}{x-1}=0\)

\(\Rightarrow5x-7=0\Leftrightarrow x=\frac{7}{5}\)( tmđk )

Vậy tập nghiệm của phuwong trình là S= { 7/5 }

b, \(\frac{x-1}{x-2}-3+x=\frac{1}{x-2}\)ĐK : x \(\ne\)2

\(\Leftrightarrow\frac{x-1}{x-2}-\left(3-x\right)=\frac{1}{x-2}\)

\(\Leftrightarrow\frac{x-1}{x-2}-\frac{\left(3-x\right)\left(x-2\right)}{x-2}=\frac{1}{x-2}\)

\(\Leftrightarrow\frac{x-1-3x+6+x^2-2x-1}{x-2}=0\)

\(\Rightarrow x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)( ktmđkxđ )

Vậy phương trình vô nghiệm 

c, \(1+\frac{1}{2+x}=\frac{12}{x^3+8}\)ĐK : x \(\ne\)-2 

\(\Leftrightarrow\frac{\left(x+2\right)\left(x^2-2x+4\right)+x^2-2x+4-12}{\left(x+2\right)\left(x^2-2x+4\right)}=0\)

\(\Rightarrow x^3+8+x^2-2x+4-12=0\)

\(\Leftrightarrow x^3+x^2-2x=0\Leftrightarrow x\left(x^2+x-2\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\left(x+2\right)=0\Leftrightarrow x=0;x=1;x=-2\left(ktm\right)\)

Vậy tập nghiệm của phương trình là S = { 0 ; 1 } 

d, đưa về dạng hđt 

Bài 2 : làm tương tự, chỉ khác ở chỗ mẫu số phức tạp hơn tí thôi 

a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23

⇔ 8x3 – 1 – 8x3 + 12x = 23

⇔ 12x = 24 ⇔ x = 2.

Tập nghiệm của phương trình: S = {2}

b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)

⇔ x ≠ -1 và x ≠ 2

Quy đồng mẫu thức hai vế :

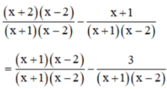
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0

Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.

a, đk : x khác 5;-6 

\(x^2+12x+36+x^2-10x+25=2x^2+23x+61\)

\(\Leftrightarrow2x+61=23x+61\Leftrightarrow21x=0\Leftrightarrow x=0\)(tm) 

b, đk : x khác 1;3 

\(x^2+2x-15=x^2-1-8\Leftrightarrow2x-15=-9\Leftrightarrow x=3\left(ktmđk\right)\)

pt vô nghiệm 

a, đk : x khác 5;-6 

(tm) 

b, đk : x khác 1;3 

x2+2x−15=x2−1−8⇔2x−15=−9⇔x=3(ktmđk)x2+2x−15=x2−1−8⇔2x−15=−9⇔x=3(ktmđk)

pt vô nghiệm 

a: \(\Leftrightarrow\left(x+6\right)^2+\left(x-5\right)^2=2x^2+23x+61\)

\(\Leftrightarrow x^2+12x+36+x^2-10x+25=2x^2+23x+61\)

=>x=0(nhận)

b: \(\Leftrightarrow\left(x+5\right)\left(x-3\right)=\left(x+1\right)\left(x-1\right)-8\)

\(\Leftrightarrow x^2+2x-15=x^2-1-8\)

=>2x-15=-9

=>2x=-6

hay x=-3(nhận)

a) \(\sqrt {11{x^2} - 14x - 12}  = \sqrt {3{x^2} + 4x - 7} \)

\(\begin{array}{l} \Rightarrow 11{x^2} - 14x - 12 = 3{x^2} + 4x - 7\\ \Rightarrow 8{x^2} - 18x - 5 = 0\end{array}\)

\( \Rightarrow x =  - \frac{1}{4}\) và \(x = \frac{5}{2}\)

Thay nghiệm vừa tìm được vào phương trình \(\sqrt {11{x^2} - 14x - 12}  = \sqrt {3{x^2} + 4x - 7} \) ta thấy chỉ có nghiệm \(x = \frac{5}{2}\) thảo mãn phương trình

Vậy nhiệm của phương trình đã cho là \(x = \frac{5}{2}\)

b) \(\sqrt {{x^2} + x - 42}  = \sqrt {2x - 30} \)

\(\begin{array}{l} \Rightarrow {x^2} + x - 42 = 2x - 3\\ \Rightarrow {x^2} - x - 12 = 0\end{array}\)

\( \Rightarrow x =  - 3\) và \(x = 4\)

Thay vào phương trình \(\sqrt {{x^2} + x - 42}  = \sqrt {2x - 30} \)  ta thấy  không có nghiệm nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

c) \(2\sqrt {{x^2} - x - 1}  = \sqrt {{x^2} + 2x + 5} \)

\(\begin{array}{l} \Rightarrow 4.\left( {{x^2} - x - 1} \right) = {x^2} + 2x + 5\\ \Rightarrow 3{x^2} - 6x - 9 = 0\end{array}\)

\( \Rightarrow x =  - 1\) và \(x = 3\)

Thay hai nghiệm trên vào phương trình \(2\sqrt {{x^2} - x - 1}  = \sqrt {{x^2} + 2x + 5} \) ta thấy cả hai nghiệm đếu thỏa mãn phương trình

Vậy nghiệm của phương trình \(2\sqrt {{x^2} - x - 1}  = \sqrt {{x^2} + 2x + 5} \) là \(x =  - 1\) và \(x = 3\)

d) \(3\sqrt {{x^2} + x - 1}  - \sqrt {7{x^2} + 2x - 5}  = 0\)

\(\begin{array}{l} \Rightarrow 3\sqrt {{x^2} + x - 1}  = \sqrt {7{x^2} + 2x - 5} \\ \Rightarrow 9.\left( {{x^2} + x - 1} \right) = 7{x^2} + 2x - 5\\ \Rightarrow 2{x^2} + 7x - 4 = 0\end{array}\)

\( \Rightarrow x =  - 4\) và \(x = \frac{1}{2}\)

Thay hai nghiệm trên vào phương trình \(3\sqrt {{x^2} + x - 1}  - \sqrt {7{x^2} + 2x - 5}  = 0\) ta thấy chỉ có nghiệm \(x =  - 4\) thỏa mãn phương trình

Vậy nghiệm của phương trình trên là \(x =  - 4\)

Câu 4:

Giả sử điều cần chứng minh là đúng

\(\Rightarrow x=y\), thay vào điều kiện ở đề bài, ta được:

\(\sqrt{x+2014}+\sqrt{2015-x}-\sqrt{2014-x}=\sqrt{x+2014}+\sqrt{2015-x}-\sqrt{2014-x}\) (luôn đúng)

Vậy điều cần chứng minh là đúng

2) \(\sqrt{x^2-5x+4}+2\sqrt{x+5}=2\sqrt{x-4}+\sqrt{x^2+4x-5}\)

⇔ \(\sqrt{\left(x-4\right)\left(x-1\right)}-2\sqrt{x-4}+2\sqrt{x+5}-\sqrt{\left(x+5\right)\left(x-1\right)}=0\)

⇔ \(\sqrt{x-4}.\left(\sqrt{x-1}-2\right)-\sqrt{x+5}\left(\sqrt{x-1}-2\right)=0\)

⇔ \(\left(\sqrt{x-4}-\sqrt{x+5}\right)\left(\sqrt{x-1}-2\right)=0\)

⇔ \(\left[{}\begin{matrix}\sqrt{x-4}-\sqrt{x+5}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}\sqrt{x-4}=\sqrt{x+5}\\\sqrt{x-1}=2\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}x\in\varnothing\\x=5\end{matrix}\right.\)

⇔ x = 5

Vậy S = {5}

Bài 1:

ĐKĐB suy ra $x(x+1)+y(y+1)=3x^2+xy-4x+2y+2$

$\Leftrightarrow 2x^2+x(y-5)+(y-y^2+2)=0$

Coi đây là PT bậc 2 ẩn $x$

$\Delta=(y-5)^2-4(y-y^2+2)=(3y-3)^2$Do đó:

$x=\frac{y+1}{2}$ hoặc $x=2-y$. Thay vào một trong 2 phương trình ban đầu ta thu được:

$(x,y)=(\frac{-4}{5}, \frac{-13}{5}); (1,1)$