Hàm số y = 2sinx +1 /1-cosx xác định khi
A. x ≠ π 2 + k 2 π
B. x ≠ k π
C. x ≠ k 2 π
D. x ≠ π 2 + k π
Những câu hỏi liên quan
Điều kiện để hàm số yfrac{1+cos x}{sin x}ysinx1+cosx xác định làxne kpi ,kin ℤ.xkπ,k∈Z.xne -pi +k2pi ,kin ℤ.x−π+k2π,k∈Z.xne frac{pi }{2}+kpi ,kin ℤ.x2π+kπ,k∈Z.xne frac{pi }{2}+k2pi ,kin ℤ.x2π+k2π,k∈Z.
Đọc tiếp
Điều kiện để hàm số y=\frac{1+\cos x}{\sin x}y=sinx1+cosx xác định là
x\ne k\pi ,k\in ℤ.x=kπ,k∈Z.
x\ne -\pi +k2\pi ,k\in ℤ.x=−π+k2π,k∈Z.
x\ne \frac{\pi }{2}+k\pi ,k\in ℤ.x=2π+kπ,k∈Z.
x\ne \frac{\pi }{2}+k2\pi ,k\in ℤ.x=2π+k2π,k∈Z.
Bạn kiểm tra lại đề bài!
Hình như đề bài ko đúng đó bn!..bn kiểm tra lại
Cho hàm số
f
(
x
)
1
+
c
o
s
x
(
x
-
π
)...
Đọc tiếp
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π/2 α π, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung
A
M
3
là A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
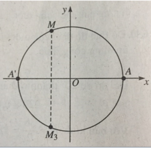
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Đúng 0
Bình luận (0)
Cho hàm số y=\(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\) với x thuộc \(\left(\dfrac{\text{π}}{4};\dfrac{\text{π}}{2}\right)\). Tìm giá trị nhỏ nhất của hàm số
y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ
Đúng 0
Bình luận (0)
Tìm tập xác định
a. y= 4/ sin22x -1
b. y= cosx-2 / sin(x/2-π/4)
Tìm tập giá trị
a. y= 4 - sin4x + cos4x
b. y= 5- 3.sinx.cosx
c. y= 4/ 5-2sinx
a) \(y=\dfrac{4}{sin^22x-1}\)
Xác định khi và chỉ khi
\(sin^22x-1\ne0\)
\(\Leftrightarrow sin^22x\ne1\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x\ne1\\sin2x\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x\ne sin\dfrac{\pi}{2}\\sin2x\ne sin\dfrac{3\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x\ne\dfrac{\pi}{2}+k2\pi\\2x\ne\dfrac{3\pi}{2}+k2\pi\\2x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{3\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow x\ne\pm\dfrac{\pi}{4}+k\pi\)
Vậy tập xác định là \(D=R\)\\(\left\{\pm\dfrac{\pi}{4}+k\pi\right\}\)
Đúng 0
Bình luận (0)
2:
a: \(y=4+\left(cos^2x-sin^2x\right)+\left(cos^2x+sin^2x\right)\)
\(=4+1+cos2x=cos2x+5\)
-1<=cos2x<=1
=>-1+5<=cos2x+5<=1+5
=>4<=cos2x+5<=6
TGT là T=[4;6]
b: \(y=5-\dfrac{3}{2}\cdot2sinx\cdot cosx=-\dfrac{3}{2}sin2x+5\)
-1<=sin 2x<=1
=>-3/2<=-3/2sin2x<=3/2
=>-3/2+5<=y<=3/2+5
=>7/2<=y<=13/2
=>TGT là T=[7/2;13/2]
c: -1<=sin x<=1
=>-2<=-2sin x<=2
=>3<=-2sinx+5<=7
=>\(\dfrac{4}{3}>=\dfrac{4}{-2sinx+5}>=\dfrac{4}{7}\)
TGT là T=[4/7;4/3]
Đúng 0
Bình luận (0)
1. Hàm số y =2sinx+cos2x , x€ [0;π) đồng biến trên khoảng nào? 2. Hàm số y=|x^2-2x-3| nghịch buến trên khoảng nào?
1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
Đúng 1
Bình luận (2)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)
Đúng 0
Bình luận (2)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π α 3π/2, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung A
M
2
là A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
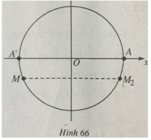
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Đúng 0
Bình luận (0)
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0
≤
x
≤
π
} và {y x + sinx, y x với
π
≤
x
≤
2
π
}b) {y sinx, y 0 với 0
≤
x
≤
π
} và {y cosx, y 0 với 0
≤
x
≤
π
};c) {y ...
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Tìm tập xác định hàm số y= √ 4 π 2 − x 2 cos x
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi A.
m
∈
{
-
3
;
1
}
. B.
m
∈
(
-
3
;
1
)
C.
m
∈
[
-
3
;
1
)
D.
m...
Đọc tiếp
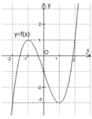
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Phương trình f(2sinx)=m có đúng ba nghiệm phân biệt thuộc đoạn [-π;π] khi và chỉ khi
A. m ∈ { - 3 ; 1 } .
B. m ∈ ( - 3 ; 1 )
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Chọn đáp án A
Phương pháp
+) Đặt t=2sinx, xác định điều kiện của t.
+) Khi đó phương trình trở thành f(t)=m. Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=m song song với trục hoành.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=m song song với trục hoành.
⇒ Phương trình f(t)=m có 1 nghiệm t=2 và một nghiệm t ∈ - 2 ; 2 hoặc phương trình f(t)=m có 1 nghiệm t=-2 và một nghiệm t ∈ - 2 ; 2 .
Đúng 0
Bình luận (0)