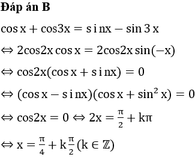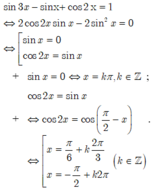Giải phương trình sau: sin 3x = 1

Những câu hỏi liên quan
Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\); b) \(\sin 3x = - \sin 5x\)
a) \(\sin x = \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{4}\;\;\;\; \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)
b)
\(\begin{array}{l}\sin 3x = - \sin 5x\;\;\;\\\; \Leftrightarrow \,\,\,\sin 3x + \sin 5x = 0\;\;\;\;\;\;\\ \Leftrightarrow \,\,\,2\sin 4x\cos x = 0\;\end{array}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = 0}\\{\cos x = 0}\end{array}\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = \sin 0}\\{\cos x = \cos \frac{\pi }{2}}\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = k\pi }\\{x = \frac{\pi }{2} + k\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.} \right.\)
Đúng 0
Bình luận (0)
Giải phương trình sau: 23sin x - sin 3x = 24
![]()
![]()
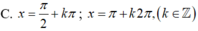
![]()
Giải phương trình sau: sin(3x + 30°) = √3/2
=>3x+30 độ=60 độ+k*360 hoặc 3x+30 độ=120 độ+k*360 độ
=>k=10 độ+k*120 độ hoặc x=30 độ+k*120 độ
Đúng 0
Bình luận (0)
Giải phương trình sau:
\(\sin\left(x\right)+\sin\left(2x\right)+4\sin\left(3x\right)+\sin\left(4x\right)+\sin\left(5x\right)=0\)
(sinx + sin5x) + (sin2x + sin4x) + 4sin3x = 0
⇔ 2sin3x . cos2x + 2sin3x . cosx + 4sin3x = 0
⇔ 2sin3x (cos2x + cosx + 2sin3x) = 0
⇔ \(\left[{}\begin{matrix}sin3x=0\left(1\right)\\cos2x+cosx+2sin3x=0\left(2\right)\end{matrix}\right.\)
(1) ⇔ ...
(2) ⇔ \(2cos\dfrac{3x}{2}.cos\dfrac{x}{2}+4sin\dfrac{3x}{2}.cos\dfrac{3x}{2}=0\)
⇔ \(\left[{}\begin{matrix}cos\dfrac{3x}{2}=0\left(\alpha\right)\\cos\dfrac{x}{2}+2sin\dfrac{3x}{2}=0\left(\beta\right)\end{matrix}\right.\)
Giải \(\left(\alpha\right)\) quá đơn giản
Giải \(\left(\beta\right)\)
\(2\left(3sin\dfrac{x}{2}-4sin^3\dfrac{x}{x}\right)+cos\dfrac{x}{2}=0\)
⇔ \(-8sin^3\dfrac{x}{2}+6sin\dfrac{x}{2}\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)+cos\dfrac{x}{2}.\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)=0\)
⇔ \(-2sin^3\dfrac{x}{2}+6sin\dfrac{x}{2}.cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}.cos\dfrac{x}{2}+cos^3\dfrac{x}{2}=0\)
Xét \(x=k2\pi,k\in Z\) tức \(sin\dfrac{x}{2}=0\) có thỏa mãn phương trình không, nếu có kết luận về nghiệm
Dù trường hợp trên có thỏa mãn hay không thì tiếp tục xét trường hợp nữa là \(x\ne k2\pi,k\in Z\) tức \(sin\dfrac{x}{2}\ne0\). Rồi chia cả 2 vế phương trình lằng nhằng kia cho \(sin\dfrac{x}{2}\) và đưa về phương trình bậc 3 theo cot\(\dfrac{x}{2}\)
Đúng 1
Bình luận (0)
Nếu tham khảo theo cách của mình thì dùng công thức này :
sin3x
= sin2x . cosx + cos2x . sinx
= 2sinx . cosx . cosx + (1 - 2sin2x) . sinx
= 2sinx . cos2x + sinx - 2sin3x
= 2sinx (1 - sin2x) + sinx - 2sin3x
= 3sinx - 4sin3x
Đúng 0
Bình luận (0)
Giải phương trình:
\(Sin^3x+Cos^3x+1=\dfrac{3}{2}Sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)+1=3sinx.cosx\)
Đặt \(sinx+cosx=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t\left(1-\dfrac{t^2-1}{2}\right)+1=\dfrac{3}{2}\left(t^2-1\right)\)
\(\Leftrightarrow t^3+3t^2-3t-5=0\)
\(\Leftrightarrow\left(t+1\right)\left(t^2+2t-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-1\\t=-1-\sqrt{6}\left(loại\right)\\t=-1+\sqrt{6}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=-\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình
cos
x
+
cos
3
x
sin
x
-
sin
3
x
.
A
.
x
-
π
4
+
k
π
2
k
∈
ℤ
B
.
x...
Đọc tiếp
Giải phương trình cos x + cos 3 x = sin x - sin 3 x .
A . x = - π 4 + k π 2 k ∈ ℤ
B . x = π 4 + k π 2 k ∈ ℤ
C . x = π 4 + k π k ∈ ℤ
D . x = π 4 + k 2 π k ∈ ℤ
câu này nhìn ngứa mắt quá làm kiểu gì giờ ???
Giải các phương trình sau: a) \(2\cos x = - \sqrt 2 \); b) \(\cos 3x - \sin 5x = 0\)
a) \(2\cos x = - \sqrt 2 \Leftrightarrow \cos x = - \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
b) \(\cos 3x - \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} - 5x} \right)\;\;\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} - 5x + k2\pi }\\{3x = - \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ - 2x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} - k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
Đúng 0
Bình luận (0)
Cho phương trình sau:
sin
3
x
-
sin
x
+
cos
2
x
1
. Phương trình có họ nghiệm
x
π
a
+
k
2
π
3
,
k
∈
ℤ
hỏi giá trị của a A. 1 B. 6 C. 3 D. 4
Đọc tiếp
Cho phương trình sau: sin 3 x - sin x + cos 2 x = 1 . Phương trình có họ nghiệm x = π a + k 2 π 3 , k ∈ ℤ hỏi giá trị của a
A. 1
B. 6
C. 3
D. 4
giải phương trình \(\frac{\tan x-\sin x}{\sin^3x}=\frac{1}{\cos x}\)