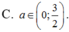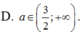Phương trình log3(2x + 1) = 2log2x+13 + 1 có hai nghiệm phân biệt . Giá trị biểu thức x1+ x2+ x1.x2 thuộc khoảng nào dưới đây
A. (0; 1)
B. (1; 2)
C. (2; 3)
D. (3; 4)
( 2 điểm )
1) Cho phương trình x2- 2x + m = 0 ( với m là số thực thoả mãn m < 1 ). Chứng minh phương trình đã cho có hai nghiệm phân biệt.
2) Cho x1 và x2 là hai nghiệm của phương trình x2+ 2x- 1 = 0.
Tính giá trị của biểu thức P = \(\dfrac{1}{x_1}\)+ \(\dfrac{1}{x_2}\)
1) \(\Delta'=1-m>0\forall m< 1\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt
2) Do a = 1; c = -1 nên a và c trái dấu
Do đó phương trình luôn có hai nghiệm phân biệt
Theo Viét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-1\end{matrix}\right.\)
\(\Rightarrow P=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_2+x_1}{x_1x_2}=\dfrac{-2}{-1}=2\)
Cho phương trình 2 x 2 + 2 m - 1 x + m 2 - 1 = 0 . Tìm giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn biểu thức A = x 1 - x 2 2 đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Biết m = m 0 là giá trị thực của tham số m sao cho phương trình 4 x - ( 4 m + 1 ) . 2 x + 2 4 m - 1 = 0 có hai nghiệm thực x 1 , x 2 thỏa mãn x 1 + 1 . x 2 + 1 = 6 . Khi đó m 0 thuộc khoảng nào sau đây?
![]()
![]()
![]()
![]()
Cho phương trình X^2 - 2(m + 1)x + m - 6 = 0 (1) , ( với m là tham số )
a> Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt x1; x2 với mọi giá trị của m
b> Tìm một hệ thức liên hệ giữa x1 ; x2 không phụ thuộc vào m
c> với giá trị nào của m thì phương trình (1) có ít nhất một nghiệm dương
a: Δ=(2m+2)^2-4(m-6)
=4m^2+8m+4-4m+24
=4m^2+4m+28
=(2m+1)^2+27>0
=>Phương trình luôn có hai nghiệm phân biệt
c: Để (1) có ít nhất 1 nghiệm dương thì
m-6<0 hoặc (2m+2>0 và m-6>0)
=>m>6 hoặc m<6
Cho phương trình x 2 − ( 2 m + 5 ) x + 2 m + 1 = 0 (1), với x là ẩn, m là tham số.
a. Giải phương trình (1) khi m= - 1 2
b. Tìm các giá trị của m để phương trình (1) có hai nghiệm dương phân biệt x 1 , x 2 sao cho biểu thức P = x 1 − x 2 đạt giá trị nhỏ nhất.
a. + Với m = − 1 2 phương trình (1) trở thành x 2 − 4 x = 0 ⇔ x = 0 x = 4 .
+ Vậy khi m = − 1 2 phương trình có hai nghiệm x= 0 và x= 4.
b. + Phương trình có hai nghiệm dương phân biệt khi
Δ = 2 m + 5 2 − 4 2 m + 1 > 0 x 1 + x 2 = 2 m + 5 > 0 x 1 . x 2 = 2 m + 1 > 0
+ Ta có Δ = 2 m + 5 2 − 4 2 m + 1 = 4 m 2 + 12 m + 21 = 2 m + 3 2 + 12 > 0 , ∀ m ∈ R
+ Giải được điều kiện m > − 1 2 (*).
+ Do P>0 nên P đạt nhỏ nhất khi P 2 nhỏ nhất.
+ Ta có P 2 = x 1 + x 2 − 2 x 1 x 2 = 2 m + 5 − 2 2 m + 1 = 2 m + 1 − 1 2 + 3 ≥ 3 ( ∀ m > − 1 2 ) ⇒ P ≥ 3 ( ∀ m > − 1 2 ) .
và P = 3 khi m= 0 (thoả mãn (*)).
+ Vậy giá trị nhỏ nhất P = 3 khi m= 0.
Biết rằng phương trình 2 x . 3 2 x + 1 x + 2 = 6 có hai nghiệm phân biệt là x1; x2. Tính giá trị của biểu thức S = x1 + x2
A. S = log 2 3 2
B. S = log 2 2 3
C. S = log 3 3 2
D. S = log 3 2 3
Chọn A.
Điều kiện: ![]()
Phương trình
![]()
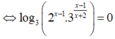
![]()
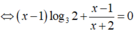
![]()
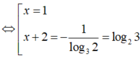
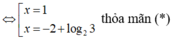
Do đó S = -1 + log23 = log23 – log22 = log23/2.
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
Giả sử phương trình log 2 2 x - ( m + 2 ) log 2 x + 2 m = 0 có hai nghiệm thực phân biệt x 1 , x 2 thỏa mãn x 1 + x 2 = 6 . Giá trị của biểu thức x 1 - x 2 là
A. 3
B. 8
C. 2
D. 4
Chọn đáp án C
Phương pháp
+) Đặt điều kiện để phương trình có nghĩa.
+) Đặt ẩn phụ để giải phương trình: log 2 x = t . Tìm điều kiện để phương trình có nghiệm.
+) Dựa vào dữ kiện x 1 + x 2 = 6 tìm m. Từ đó tính x 1 - x 2 .
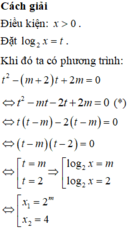
Phương trình đã cho có hai nghiệm phân biệt: x 1 , x 2 ⇔ phương trình (*) có hai nghiệm phân biệt ⇔ m ≠ 2 .
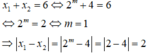
Phương trình
1 + 2 x + 1 - 2 a 2 - 1 x - 4 = 0 có 2 nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 - x 2 = log 1 + 2 3 . Mệnh đề nào dưới đây đúng?