Khoảng cách giữa hai đường thẳng d 1 : 6 x - 4 y + 5 = 0 v à d 2 : 3 x - 2 y + 1 = 0 bằng bao nhiêu?
A. 6 52
B. 5 52
C. 4 52
D. 3 52
Cho hai đường thẳng (d): 2x-y-2=0 và (d’): 4x-2y+6=0.Khoảng cách giữa hai đường thẳng là:
\(A,-\sqrt{5}\)
\(B,2\sqrt{5}\)
\(C\sqrt{5}\)
D.5
NX: \(\dfrac{2}{4}\)=\(\dfrac{-1}{-2}\)≠\(\dfrac{-2}{6}\)
=> (d) // (d')
Ta lấy điểm A(0;-2) ∈ d
d(d;d') = \(\dfrac{\left|4.0-2.\left(-2\right)+6\right|}{\sqrt{4^2+2^2}}\) = \(\sqrt{5}\)
=> Chọn C
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\)và \({\Delta _2}:x - y - 1 = 0\)
a) Ta có: \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1 \Leftrightarrow x - 2y + 4 = 0\)
Vậy khoảng cách từ O đến \(\Delta \) là: \(d\left( {O;\Delta } \right) = \frac{{\left| {1.0 - 2.0 + 4} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \frac{{4\sqrt 5 }}{5}\)
b) Lấy \(M\left( {0;1} \right) \in {\Delta _1}\)
Suy ra: \(d\left( {{\Delta _1},{\Delta _2}} \right) = d\left( {M,{\Delta _2}} \right) = \frac{{\left| {0 - 1 - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 2 \)
Câu 1: Tìm tập hợp các điểm cách đều 2 đường thẳng:
Delta3 :3x + 4 y + 6 = 0
Delta4 :5x -10 = 0 ( phân giác góc tạo bởi D3 và D4 )
Câu 2: Cho hai đường thẳng:
Delta : 3x + 2y - 1 = 0 và d : 5x - 3y+2=0
1) Tính khoảng cách từ A(5 ;4) đến đường thẳng Delta
2) Viết phương trình các đường phân giác của góc tạo bởi hai đường thẳng trên.
3) Tìm điểm M thuộc Delta sao cho khoảng cách từ M đến d bằng 5.
4) Tìm điểm N thuộc đường thẳng (D1) : x - 2y = 0 bằng hai lần khoảng cách từ N đến d .
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng chéo nhau ∆ : x - 2 2 = y - 3 - 4 = z - 1 - 5 và d : x - 1 1 = y - 2 = z + 1 2 . Khoảng cách giữa hai đường thẳng ∆ và d bằng
A. 5 5
B. 45 14
C. 5
D. 3
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Trong không gian Oxyz, khoảng cách giữa đường thẳng d : x + 1 - 2 = y - 2 2 = z + 3 3 và mặt phẳng (P): x-2y+2z-5=0 bằng
A. 16 3
B. 2
C. 5 3
D. 3
Trong không gian Oxyz, khoảng cách giữa hai đường thẳng d 1 : x + 7 3 = y - 5 - 1 = z - 9 4 và d 2 : x 3 = y + 4 - 1 = z + 18 4 bằng
A. 30.
B. 20.
C. 25.
D. 15.
KHoảng cách giữa 2 đường thẳng d: 2x - y +3 =0 và d' \(\left\{{}\begin{matrix}x=3+t\\y=4+2t\end{matrix}\right.\)
Cho hai đường thẳng
∆ : x - 1 2 = y + 3 1 = z - 4 - 2 ∆ ' : x + 2 - 4 = y - 1 - 2 = z + 1 4
Tính khoảng cách giữa ∆ và ∆ ′.
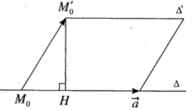
Ta có M 0 M ' 0 → = (−3; 4; −5)
a → = (2; 1; −2)
n → = M 0 M ' 0 → ∧ a → = (−3; −16; −11)
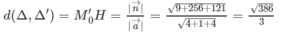
Trong không gian Oxyz, cho hai đường thẳng: d 1 : x - 3 - 4 = y + 2 1 = z + 1 1 và d 2 : x - 6 = y - 1 1 = z - 2 2 . Khoảng cách giữa chúng bằng
A. 5.
B. 4.
C. 2.
D. 3.