Cho đường thẳng d có phương trình tham số x = 2 - 3 t y = - 1 + 2 t ( t ∈ ℝ ) và điểm A(3,5 ; -2). Điểm A thuộc d ứng với giá trị nào của t ?
Những câu hỏi liên quan
Đường thẳng (d) có phương trình tham số:
x
2
-
3
t
y
1
+
t
Phương trình tổng quát của đường thẳng (d) là A. x+3y+50 B. -3x+y-70 C. -3x+y+50 D. x+3y-50
Đọc tiếp
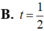
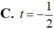
Đường thẳng (d) có phương trình tham số: x = 2 - 3 t y = 1 + t Phương trình tổng quát của đường thẳng (d) là
A. x+3y+5=0
B. -3x+y-7=0
C. -3x+y+5=0
D. x+3y-5=0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
-
3
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = - 3 t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương 
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
3
-
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = 3 - t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương 
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình tham số là
x
-
1
+
3
t
y
2
-
t
. Phương trình tổng quát của d là: A.
3
x
-
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình tham số là x = - 1 + 3 t y = 2 - t . Phương trình tổng quát của d là:
A. 3 x - y + 5 = 0
B. x + 3 y = 0
C. x + 3 y - 5 = 0
D. 3 x - y + 2 = 0
Cho đường thẳng d có phương trình tham số là: \(\left\{ \begin{array}{l}x = - 1 - 3t\\y = 2 + 2t\end{array} \right.\)
a) Lập phương trình tổng quát của đường thẳng d.
b) Tìm toạ độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.
c) Đường thẳng d có đi qua điểm M(-7; 5) hay không?
a) Xét phương trình tham số của d: \(\left\{ \begin{array}{l}x = - 1 - 3t\left( 1 \right)\\y = 2 + 2t\left( 2 \right)\end{array} \right.\).
Lấy \(\left( 1 \right) + \frac{3}{2}.\left( 2 \right) \Rightarrow x + \frac{3}{2}y = 2 \Rightarrow 2x + 3y - 4 = 0\)
Vậy phương trình tổng quát của đường thẳng d là: \(2x + 3y - 4 = 0\)
b) Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{4}{3}\\x = 0\end{array} \right.\) . Vậy giao điểm của d với trục Oy là: \(A\left( {0;\frac{4}{3}} \right)\)
Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 2\end{array} \right.\) . Vậy giao điểm của d với trục Ox là: \(B\left( {2;0} \right)\)
c) Thay tọa độ điểm \(M\left( { - 7;{\rm{ }}5} \right)\)vào phương trình đường thẳng d ta có: \(2.\left( { - 7} \right) + 3.5 - 4 \ne 0\)
Vậy \(M\left( { - 7;{\rm{ }}5} \right)\)không thuộc đường thẳng d.
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxyz, cho đường thẳng d:
x
-
1
1
y
-
2
-
2
z
+
2
3
. Phương trình nào sau đây là phương trình tham số của d?
Đọc tiếp
Trong hệ tọa độ Oxyz, cho đường thẳng d: x - 1 1 = y - 2 - 2 = z + 2 3 . Phương trình nào sau đây là phương trình tham số của d?
Đường thẳng d có phương trình chính tắc
x
+
1
-
3
y
-
2
1
.Phương trình nào sau đây là phương trình tham số của d?
Đọc tiếp
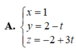
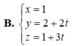
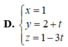
Đường thẳng d có phương trình chính tắc x + 1 - 3 = y - 2 1 .Phương trình nào sau đây là phương trình tham số của d?
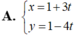
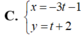
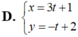
Đường thẳng d có 
và đi qua điểm M(-1; 2)
Vậy phương trình tham số của đường thẳng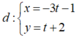 
.
Chọn C.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y2x2�2�2 và đường thẳng (d) có phương trình y2(m−1)x−m+�2(�−1)�−�+ 1, trong đó m là tham số. a, Vẽ parabol (P).b, Xác đị...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình
và đường thẳng (d) có phương trình
1, trong đó m là tham số.
a, Vẽ parabol (P).
b, Xác định m để đường thẳng (d) cắt (P) tại hai điểm phân biệt.
c, Chứng minh rằng khi m thay đổi, các đường thẳng (d) luôn đi qua một điểm cố định
a:
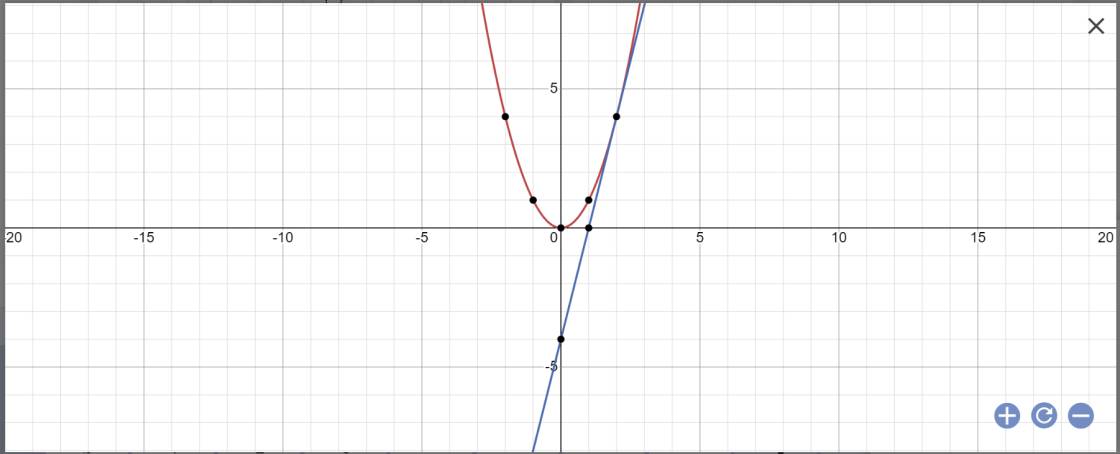
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
Đúng 0
Bình luận (0)
Cho hai đường thẳng d và d có phương trình tham số lần lượt là
x
3
+
2
t
y
6
+
4
t
z...
Đọc tiếp
Cho hai đường thẳng d và d' có phương trình tham số lần lượt là x = 3 + 2 t y = 6 + 4 t z = 4 + t v à x = 2 + t ' y = 1 - t ' z = 5 + 2 t '
Hãy chứng tỏ d và d’ có hai vecto chỉ phương không cùng phương.
a d → = (2;4;1); a d ' → = (1;-1;2) là hai vecto không tỉ lệ nên hai veco đó không cùng phương
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho đường thẳng Δ có phương trình
x
−
2
1
y
+
3
2
z
−
1
3
. Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng
O
y...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng Δ có phương trình x − 2 1 = y + 3 2 = z − 1 3 . Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng O y z .
A. x = 0 y = 3 + 2 t z = − 1 + 3 t
B. x = 0 y = − 3 + 2 t z = 1 + 3 t
C. x = − 2 + t y = 0 z = 0
D. x = 2 + t y = 0 z = 0
Đáp án B.
Δ : x − 2 1 = y + 3 2 = z − 1 3
Lấy M 2 ; − 3 ; 1 và N 3 ; − 1 ; 4 là hai điểm thuộc Δ.
⇒ M ' 0 ; − 3 ; 1 và N ' 0 ; − 1 ; 4 lần lượt là hình chiếu của hai điểm M; N trên mặt phẳng (Oxy)
⇒ u d → = M ' N ' → = 0 ; 2 ; 3 ⇒ d : x = 0 y = − 3 + 2 t z = 1 + 3 t
Đúng 0
Bình luận (0)