a d → = (2;4;1); a d ' → = (1;-1;2) là hai vecto không tỉ lệ nên hai veco đó không cùng phương
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với tin Rt∈R)A,left{{}begin{matrix}x2+2ty7+4tz1+3tend{matrix}right.⎩⎪⎨⎪⎧x2+2ty7+4tz1+3tB,left{{}begin{matrix}x4y3+3tz2-2tend{matrix}right.⎩⎪⎨⎪⎧x4y3+3tz2−2tc,left{{}begin{matrix}x2y4-3tz3+2tend{matrix}right.⎩⎪⎨⎪⎧x2y4−3tz3+2td,left{{}begin{matrix}x2+2ty4+7tz3+tend{matrix}right.⎩⎪⎨⎪⎧x2+2ty4+7tz3+t
Đọc tiếp
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với t\in \Rt∈R)
A,\left\{{}\begin{matrix}x=2+2t\\y=7+4t\\z=1+3t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=7+4tz=1+3t
B,\left\{{}\begin{matrix}x=4\\y=3+3t\\z=2-2t\end{matrix}\right.⎩⎪⎨⎪⎧x=4y=3+3tz=2−2t
c,\left\{{}\begin{matrix}x=2\\y=4-3t\\z=3+2t\end{matrix}\right.⎩⎪⎨⎪⎧x=2y=4−3tz=3+2t
d,\left\{{}\begin{matrix}x=2+2t\\y=4+7t\\z=3+t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=4+7tz=3+t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
v
à
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 v à ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng ∆1;∆2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
2
2
+
z
-
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 4 . Xét đường thẳng d : x = 1 + t y = - m t z = ( m - 1 ) t với m là tham số thực. Giả sử (P) và (P') là hai mặt phẳng chứa d, tiếp xúc với (S) lần lượt tại T và T'. Khi m thay đổi, tính giá trị nhỏ nhất của độ dài đoạn thẳng TT'.
A. 2
B. 2 11 3
C. 4 13 5
D. 2 2
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
và
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
và
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Cho hai đường thẳng d và d có phương trình tham số lần lượt là
x
3
+
2
t
y
6
+
4
t
z...
Đọc tiếp
Cho hai đường thẳng d và d' có phương trình tham số lần lượt là x = 3 + 2 t y = 6 + 4 t z = 4 + t v à x = 2 + t ' y = 1 - t ' z = 5 + 2 t '
Hãy chứng tỏ điểm M(1; 2; 3) là điểm chung của d và d’
Trong không gian tọa độ Oxyz cho đường thẳng
d
1
và
d
2
lần lượt có phương trình
x
9
+
2
t
y
-
1
-...
Đọc tiếp
Trong không gian tọa độ Oxyz cho đường thẳng d 1 và d 2 lần lượt có phương trình x = 9 + 2 t y = - 1 - t z = 3 - t và x = 1 - 2 t ' y = 4 + t ' z = 2 + t ' Viết phương trình mặt phẳng chứa cả hai đường thẳng d 1 và d 2
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là
x
1
y
+
1
2
z
1
v
à
x
1
y
-
1
-
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là x 1 = y + 1 2 = z 1 v à x 1 = y - 1 - 2 = z - 1 3 .Đường thẳng d cắt cả hai đường thẳng d₁, d₂ và song song với đường thẳng ∆ : x - 4 1 = y - 7 4 = z - 3 - 2 có phương trình là:
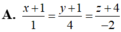
![]()
![]()
![]()
Trong không gian Oxyz cho mặt cầu (S): (x-3)²+ (y-1)²+z² 4 và đường thẳng
d
:
x
1
+
2
t
y
-
1
+
t
,...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S): (x-3)²+ (y-1)²+z² = 4 và đường thẳng d : x = 1 + 2 t y = - 1 + t , t ∈ ℝ z = - t . Mặt phẳng chứa d và cắt (S) theo một đường tròn có bán kính nhỏ nhất có phương trình là:
A. 3x-2y-4z-8=0
B. y+z+1=0
C. x-2y-3=0
D. x+3y+5z+2=0




