Giả sử lim x → a + f ( x ) = + ∞ và lim x → a + g ( x ) = - ∞ . Xét các mệnh đề sau:
lim x → a + f ( x ) - g ( x ) = + ∞
lim x → a + f ( x ) g ( x ) = - 1
lim x → a + f ( x ) + g ( x ) = 0 . Số mệnh đề đúng là:
A.0
B.1
C.2
D.3
Những câu hỏi liên quan
Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 12:55
Cho hai hàm số và y gleft( x right) frac{x}{{x + 1}}.a) Giả sử left( {{x_n}} right) là dãy số bất kì thoả mãn {x_n} ne - 1 với mọi n và {x_n} to 1 khi n to + infty . Tìm giới hạn lim left[ {fleft( {{x_n}} right) + gleft( {{x_n}} right)} right].b) Từ đó, tìm giới hạn mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right], và so sánh với mathop {lim }limits_{x to 1} {rm{ }}fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).
Đọc tiếp
Cho hai hàm số và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).
b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
a) \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \lim \left( {2{x_n} + \frac{{{x_n}}}{{{x_n} + 1}}} \right) = 2\lim {x_n} + \lim \frac{{{x_n}}}{{{x_n} + 1}} = 2.1 + \frac{1}{{1 + 1}} = \frac{5}{2}\)
b) Vì \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \frac{5}{2}\) nên \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \frac{5}{2}\) (1).
Ta có: \(\lim {\rm{ }}f\left( {{x_n}} \right) = \lim 2{x_n} = 2\lim {x_n} = 2.1 = 2 \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) = 2\)
\(\lim g\left( {{x_n}} \right) = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \frac{1}{{1 + 1}} = \frac{1}{2} \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}g\left( x \right) = \frac{1}{2}\)
Vậy \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2 + \frac{1}{2} = \frac{5}{2}\) (2).
Từ (1) và (2) suy ra \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\)
Đúng 0
Bình luận (0)
giải thích bằng định nghĩa: lim f(x)=2 khi x->-00 và lim g(x)=3 khi x->-00 .từ các giả thiết dã cho bằng đình ngĩa chứng minh lim (f(x) +g(x))= 5 khi x->-00.
e xin cảm ơn trước ạ
Lời giải:
Theo định nghĩa về giới hạn thì khi \(\lim_{x\to -\infty}f(x)=2; \lim_{x\to -\infty}g(x)=3\) thì \(\lim_{x\to -\infty}[f(x)-2]=0; \lim_{x\to -\infty}[g(x)-3]=0\)
Khi đó, theo định nghĩa về giới hạn 0 thì với mọi số \(\epsilon >0\) ta tìm được tương ứng $n_1,n_2$ sao cho:
\(\left\{\begin{matrix} |f(x)-2|<\frac{\epsilon}{2}\forall n>n_1\\ |g(x)-3|< \frac{\epsilon}{2}\forall n>n_2\end{matrix}\right.\)
Gọi \(n_0=\max (n_1,n_2)\)
\(\Rightarrow |f(x)-2+g(x)-3|< |f(x)-2|+|g(x)-3|< \frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon \) \(\forall n>n_0\)
Điều này chứng tỏ \(f(x)-2+g(x)-3=f(x)+g(x)-5\) có giới hạn 0
\(\Rightarrow \lim_{x\to -\infty}[f(x)+g(x)]=5\)
Đúng 0
Bình luận (0)
Biết lim x -> +∞ f(x) = M ;lim x -> +∞ g(x) = 0 Chọn khẳng định đúng? A. Lim x -> +∞ f(x)/g(x)= +∞ B. Lim x -> +∞ = f(x)/g(x)= -∞ C. Lim x -> +∞ f(x)/g(x)=0 D. Limx -> +∞ [g(x).f(x)]=0
cho \(f\left(x\right)=\left\{{}\begin{matrix}x^2-3\\x+3\end{matrix}\right.\) \(x\ge3\);\(x< 3\)
a) tính \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=?\)
\(\lim\limits_{x\rightarrow3^-}f\left(x\right)=?\)
b) tính \(\lim\limits_{x\rightarrow3}f\left(x\right)\) nếu có
a: \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^+}x^2-3=3^2-3=6\)
\(\lim\limits_{x\rightarrow3^-}f\left(x\right)=\lim\limits_{x\rightarrow3^-}x+3=3+3=6\)
b: Vì \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)=6\)
nên hàm số tồn tại lim khi x=3
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=6\)
Đúng 3
Bình luận (0)
Cho hàm số f(x) liên tục và a0. Giả sử với mọi
x
∈
0
;
a
ta có f(x)0 và f(x).f(a-x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
Đọc tiếp
Cho hàm số f(x) liên tục và a>0. Giả sử với mọi x ∈ 0 ; a ta có f(x)>0 và f(x).f(a-x) = 1. Tính I = ∫ 0 a d x 1 + f ( x )
Cho hai hàm số fleft( x right) {x^2} - 1,gleft( x right) x + 1.a) Tính mathop {lim }limits_{x to 1} fleft( x right) và mathop {lim }limits_{x to 1} gleft( x right).b) Tính mathop {lim }limits_{x to 1} left[ {fleft( x right) + gleft( x right)} right]và so sánh mathop {lim }limits_{x to 1} fleft( x right) + mathop {lim }limits_{x to 1} gleft( x right).c) Tính mathop {lim }limits_{x to 1} left[ {fleft( x right) - gleft( x right)} right]và so sánh mathop {lim }limits_{x to 1} fleft( x right) - mat...
Đọc tiếp
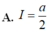
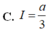
Cho hai hàm số \(f\left( x \right) = {x^2} - 1,g\left( x \right) = x + 1.\)
a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
b) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
c) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
d) Tính \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right]\)và so sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\)
e) Tính \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}}\)và so sánh \(\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\)
a) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - 1} \right) = \mathop {\lim }\limits_{x \to 1} {x^2} - \mathop {\lim }\limits_{x \to 1} 1 = {1^2} - 1 = 0\)
\(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to 1} x + \mathop {\lim }\limits_{x \to 1} 1 = 1 + 1 = 2\)
b) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x} \right) = {1^2} + 1 = 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 + 2 = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
c) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} - x - 2} \right) = {1^2} - 1 - 2 = - 2\\\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 - 2 = - 2\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
Đúng 0
Bình luận (0)
d) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left[ {\left( {{x^2} - 1} \right)\left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + {x^2} - x - 1} \right) = {1^3} + {1^2} - 1 - 1 = 0\\\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0.2 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right).\end{array}\)
e) \(\begin{array}{l}\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x - 1} \right) = 1 - 1 = 0\\\frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}} = \frac{0}{2} = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}.\end{array}\)
Đúng 0
Bình luận (0)
Cho f(x) là hàm liên tục và a0. Giả sử rằng với mọi x thuộc [0;a] ta có f(x)0 và f(x).f(a-x) 1 Hãy tính
I
∫
0
a
d
x
1
+
f
(
x
)
theo a. A. a. B.
a
2
C. 2a D. 3a
Đọc tiếp
Cho f(x) là hàm liên tục và a>0. Giả sử rằng với mọi x thuộc [0;a] ta có f(x)>0 và f(x).f(a-x) = 1 Hãy tính I = ∫ 0 a d x 1 + f ( x ) theo a.
A. a.
B. a 2
C. 2a
D. 3a
Cho hàm số y f(x) liên tục trên R và a 0. Giả sử rằng với mọi
x
∈
0
;
a
, ta có f(x) 0 và f(x)f(a – x) 1. Tính
I
∫
0
a
d
x
1
+
f
(
x
)
. A.
a...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và a > 0. Giả sử rằng với mọi x ∈ 0 ; a , ta có f(x) > 0 và f(x)f(a – x) = 1. Tính I = ∫ 0 a d x 1 + f ( x ) .
A. a 2 .
B. 2a.
C. a 3 .
D. aln(a + 1).
Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
Đúng 0
Bình luận (0)
Giải mục 1 trang 111, 112, 113 SGK Toán 11 tập 1 - Kết nối tri thức
16 tháng 7 2023 lúc 16:06
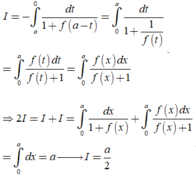
Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.
Giả sử \(\left( {{x_n}} \right)\) là dãy số sao cho \({x_n} > 1,\;{x_n} \to \; + \infty \). Tính \(f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
