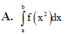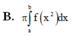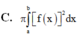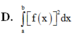Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
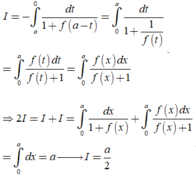
Chọn A.
Từ giả thiết, suy ra f a - x = 1 f x
Đặt t=a-x suy ra dt=-dx . Đổi cận: x = 0 → t = a x = a → t = 0
Khi đó
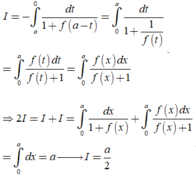
Cho hàm số f(x) liên tục và a>0. Giả sử với mọi x ∈ 0 ; a ta có f(x)>0 và f(x).f(a-x) = 1. Tính I = ∫ 0 a d x 1 + f ( x )
![]()
![]()
Cho f(x) là hàm liên tục và a>0. Giả sử rằng với mọi x thuộc [0;a] ta có f(x)>0 và f(x).f(a-x) = 1 Hãy tính I = ∫ 0 a d x 1 + f ( x ) theo a.
A. a.
B. a 2
C. 2a
D. 3a
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).(fa-x) = 1 Tính tích phân ∫ 0 1 1 1 + f ( x ) d x
A. I = a/2
B. I = a
C. I = 2a/3
D. I = a/3
Cho số thực a>0 Gỉa sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a-x) = 1 Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
A. a/3
B. a/2
C. a
D. 2a/3
Cho hàm số f(x) xác định và có đạo hàm f'(x) liên tục trên đoạn [1;3], f x ≠ 0 với mọi x ∈ 1 ; 3 , đồng thời f ' x 1 + f x 2 = f x 2 x - 1 2 và f(1) = -1
Biết rằng ∫ 1 3 f x d x = a ln 3 + b , a , b ∈ Z , tính tổng S = a + b 2
A. S = 0
B. S = -1
C. S = 2
D. S = 4
Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên 0 ; + ∞ và thỏa mãn f(1)=1, f ( x ) = f ' ( x ) 3 x + 1 , với mọi x>0. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
∫ - a a f x d x = 2 ∫ 0 a f x d x 1 0 2
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính: ∫ - 2 2 ln x + 1 + x 2 d x
Cho hàm số y = f(x) xác định và liên tục trên R \ 0 biết x . f x ≠ - 1 ∀ x ≠ 0 f(1) = -2 và với ∀ x ∈ R \ 0 Tính ∫ 1 e f x d x
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và f(x)>0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và 2 đường thẳng x=a; x=b Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức