Tính giá trị biểu thức K = log a a a với 0 < a ≠ 1
A. K = 4 3
B. K = 3 8
C. K = 4 3
D. K = 1
a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
Cho \(0 < a \ne 1\). Tính giá trị của biểu thức \(B = {\log _a}\left( {\frac{{{a^2} \cdot \sqrt[3]{a} \cdot \sqrt[5]{{{a^4}}}}}{{\sqrt[4]{a}}}} \right) + {a^{2{{\log }_a}\frac{{\sqrt {105} }}{{30}}}}\).
\(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}=\dfrac{a^2\cdot a^{\dfrac{1}{3}}\cdot a^{\dfrac{4}{5}}}{a^{\dfrac{1}{4}}}=\dfrac{a^{\dfrac{47}{15}}}{a^{\dfrac{1}{4}}}=a^{\dfrac{173}{60}}\)
\(\Rightarrow log_a\left(\dfrac{a^2\cdot\sqrt[3]{a}\cdot\sqrt[5]{a^4}}{\sqrt[4]{a}}\right)=log_a\left(a^{\dfrac{173}{60}}\right)=\dfrac{173}{60}\)
\(a^{2log_a\left(\dfrac{\sqrt{105}}{30}\right)}=a^{log_a\left(\dfrac{7}{60}\right)}=\dfrac{7}{60}\)
Vậy \(B=\dfrac{173}{60}+\dfrac{7}{60}=\dfrac{180}{60}=3\)
Đề bài
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 100\). Tính giá trị của biểu thức \(P = 3\log a + 2\log b\)
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
Tính giá trị của các biểu thức sau:
a) \(A = {\log _2}3.{\log _3}4.{\log _4}5.{\log _5}6.{\log _6}7.{\log _7}8;\)
b) \(B = {\log _2}2.{\log _2}4...{\log _2}{2^n}.\)
\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
\(=\left(log_{a^{-1}}a^2\right)^2+\dfrac{1}{2}.\dfrac{1}{2}log_aa\)
\(=\left(-1.2.log_aa\right)^2+\dfrac{1}{4}=4+\dfrac{1}{4}=\dfrac{17}{4}\)
Tính giá trị của biểu thức :
K = a 1 6 + b 1 6 a 1 2 - b 1 2 a 1 2 - a - 1 6 b 1 6 + b 1 2
với a,b > 0
A. K = a + b
B. K = a - b
C. K = 1 + a b a
D K = 1 - a b a .
Đặt x = a - 1 6 ; y = b - 1 6 . Khi đó
K = x + y x 2 - x y + y 2 x 3 - y 3 = x 3 + y 3 x 3 - y 3 = x 6 - y 6 = a - 1 - b = 1 - a b a
Đáp án D
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):
a) \({\log _3}15\);
b) \(\log 8 - \log 3\);
c) \(3\ln 2\).
a) \(log_315=2,4650\)
c) \(3In2=2,0794\)
Tính giá trị của biểu thức K = log a a a với 0 < a ≠ 1 ta được kết quả
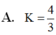
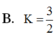
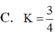

Tính giá trị của biểu thức K = log a a a với 0 < a ≠ 1 ta được kết quả
A. K = 4 3
B. K = 3 2
C. K = 3 4
D. K = − 3 4