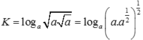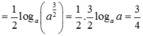Các câu hỏi tương tự
Tính giá trị của biểu thức
K
log
a
a
a
với
0
a
≠
1
ta được kết quả
Đọc tiếp
Tính giá trị của biểu thức K = log a a a với 0 < a ≠ 1 ta được kết quả
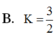
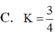

Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Trong không gian Oxyz cho mặt phẳng (P): 2x-y+2z-140 và mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
4
y
+
2
z
-
3
0
. Gọi tọa độ điểm M(a;b;c) thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Tính giá trị biểu thức Ka+b+c A. K1 B. K2 C. K-5 D. K-...
Đọc tiếp
Trong không gian Oxyz cho mặt phẳng (P): 2x-y+2z-14=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Gọi tọa độ điểm M(a;b;c) thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Tính giá trị biểu thức K=a+b+c
A. K=1
B. K=2
C. K=-5
D. K=-2
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1? A. k 2 B. k -1 C. k 1 D. Đáp án khác
Đọc tiếp
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y= x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1?
A. k =2
B. k= -1
C. k= 1
D. Đáp án khác
Cho phương trình
9
x
+
9
-
x
14
. Tính giá trị của biểu thức
K
8
+
3
x
+
3
-
x
1
-...
Đọc tiếp
Cho phương trình 9 x + 9 - x = 14 . Tính giá trị của biểu thức K = 8 + 3 x + 3 - x 1 - 3 x - 3 - x .
A. - 5 2
B. - 4
C. 2
D. 4 5
Cho đồ thị C: y 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là A.
k
9
8
k
≠
0
B.
k...
Đọc tiếp
Cho đồ thị C: y= 2x3-3x2-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là
A. k < 9 8 k ≠ 0
B. k > - 9 8 k ≠ 0
C. k < - 9 8 k ≠ 0
D. k > 9 8 k ≠ 0
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. {0} B. R C. {-3} D. (-3; +∞).
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. {0}
B. R
C. {-3}
D. (-3; +∞).
Cho hàm số yx3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. 4 B. 1 C. 6 D. vô số
Đọc tiếp
Cho hàm số y=x3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. 4
B. 1
C. 6
D. vô số
Nếu log(log(log(logx))) = 0 thì x = 10 k . Tìm giá trị của k?
A. 10
B. 100
C. 10 3
D. 10 10