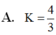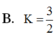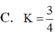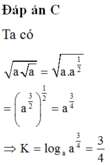Các câu hỏi tương tự
Tính tích phân
I
∫
0
2
3
x
+
x
-
4
d
x
ta được kết quả
I
a
+
b
ln
c
( với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức
T...
Đọc tiếp
Tính tích phân I = ∫ 0 2 3 x + x - 4 d x ta được kết quả I = a + b ln c ( với a, b, c là các số nguyên dương). Khi đó giá trị của biểu thức T = a 3 + 3 b 2 + 2 c bằng:
A. 55
B. 36
C. 38
D. 73
Tính tích phân
I
∫
-
2
0
x
2
-
x
-
2
x
-
1
d
x
ta được kết quả I a + bln2 + cln3 ( với a, b, c là các số nguyên). Khi đó giá trị...
Đọc tiếp
Tính tích phân I = ∫ - 2 0 x 2 - x - 2 x - 1 d x ta được kết quả I = a + bln2 + cln3 ( với a, b, c là các số nguyên). Khi đó giá trị của biểu thức T = 2 a 3 + 3 b - 4 c là:
A. T = -20.
B. T = 3.
C. T = 22.
D. T = 6.
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Rút gọn biểu thức
A
a
4
log
a
2
3
với
0
a
≠
1
ta được kết quả là A. 9 B.
3
4
C.
3
8
D. 6
Đọc tiếp
Rút gọn biểu thức A = a 4 log a 2 3 với 0 < a ≠ 1 ta được kết quả là
A. 9
B. 3 4
C. 3 8
D. 6
Tính giá trị biểu thức
K
log
a
a
a
với
0
a
≠
1
A.
K
4
3
B.
K
3
8
C.
K
4
3
D.
K...
Đọc tiếp
Tính giá trị biểu thức K = log a a a với 0 < a ≠ 1
A. K = 4 3
B. K = 3 8
C. K = 4 3
D. K = 1
Tính tích phân
I
∫
0
1
x
x
-
a
d
x
,
a
0
ta được kết quả If(a). Khi đó tổng
f
8
+
f
1
2
có giá trị bằng: A.
24
91
. B....
Đọc tiếp
Tính tích phân I = ∫ 0 1 x x - a d x , a > 0 ta được kết quả I=f(a). Khi đó tổng f 8 + f 1 2 có giá trị bằng:
A. 24 91 .
B. 91 24 .
C. 17 2 .
D. 2 17 .
Tính giá trị của biểu thức
S
log
1
2
+
log
2
3
log
3
4
+
.
.
.
+
log
99
100
A.
1
10
B.
-
1
10
C. 2...
Đọc tiếp
Tính giá trị của biểu thức S = log 1 2 + log 2 3 = log 3 4 + . . . + log 99 100
A. 1 10
B. - 1 10
C. 2
D. -2
Tính giá trị của biểu thức
P
log
(
tan
1
0
)
+
log
(
tan
2
0
)
+
log
(
tan
3
0
)
+
.
.
.
+
log
(
tan
89
0
)
.
Đọc tiếp
Tính giá trị của biểu thức P = log ( tan 1 0 ) + log ( tan 2 0 ) + log ( tan 3 0 ) + . . . + log ( tan 89 0 ) .
![]()
![]()
![]()
![]()
Cho
f
x
a
ln
x
+
x
2
+
1
+
b
sin
x
+
6
với
a
,
b
∈
ℝ
. Biết rằng f(log(log e)) 2. Tính giá trị của f(log(ln10)). A. 10 B. 2 C. 4 D. 8
Đọc tiếp
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8