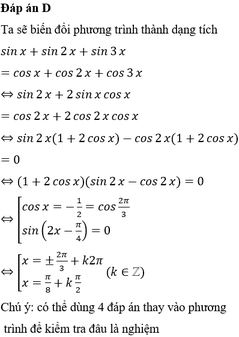b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)

\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)

c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)

\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)

\(3sinx-4sin^3x-4cos^3x+3cosx+\left(sinx+cosx\right)^2=0\)

\(\Leftrightarrow3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)+\left(sinx+cosx\right)^2=0\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(3-4+4sinx.cosx+sinx+cosx\right)=0\)

Xét \(sinx+cosx+4sinx.cosx-1=0\)

Đặt \(sinx+cosx=t\) (\(\left|t\right|\le\sqrt{2}\)) \(\Rightarrow2sinx.cosx=t^2-1\)

\(\Rightarrow2\left(t^2-1\right)+t-1=0\)

\( 2)\sin x + \sin 2x + \sin 3x = 0\\ \Leftrightarrow 2\sin 2x.\cos x + \sin 2x = 0\\ \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 2x = 0\\ 2\cos x + 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 2x = k\pi \\ \cos x = \dfrac{{ - 1}}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{k\pi }}{2}\\ x = \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z} } \right) \)

\( 3)\sin x + \sin 2x + \sin 3x + \sin 4x = 0\\ \Leftrightarrow \left( {\sin x + \sin 4x} \right) + \left( {\sin 2x + \sin 3x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{5x}}{2}.\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{5x}}{2}.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.\left( {\cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.2\cos x.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin \dfrac{{5x}}{2} = 0\\ 2\cos x = 0\\ \cos \dfrac{x}{2} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2k\pi }}{5}\\ x = \dfrac{\pi }{2} + k\pi \\ x = \pi + 2k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \)

a.

\(\Leftrightarrow\frac{2}{\sqrt{5}}sinx-\frac{1}{\sqrt{5}}cosx=\frac{2}{\sqrt{5}}\)

Đặt \(\frac{2}{\sqrt{5}}=cosa\) với \(a\in\left(0;\pi\right)\)

\(\Rightarrow sinx.cosa-cosx.sina=cosa\)

\(\Leftrightarrow sin\left(x-a\right)=sin\left(\frac{\pi}{2}-a\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-a=\frac{\pi}{2}-a+k2\pi\\x-a=\frac{\pi}{2}+a+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{\pi}{2}+2a+k2\pi\end{matrix}\right.\)

b.

\(\Leftrightarrow\sqrt{2}sin\left(3x+\frac{\pi}{4}\right)=1\)

\(\Leftrightarrow sin\left(3x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\3x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow...\)

c.

\(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x=\frac{1}{2}\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=\frac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow...\)

Câu cuối là \(-cosx\) hay \(-cos2x\) bạn?

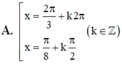
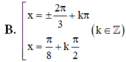
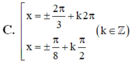
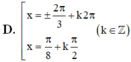
Chọn D

Ta sẽ biến đổi phương trình thành dạng tích

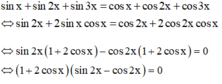
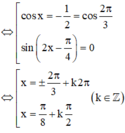
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

\(pt\Leftrightarrow\left(cosx+sinx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=cosx+sinx+sin2x\)

\(\Leftrightarrow\left(cosx+sinx\right)\left(1-sinx.cosx-1\right)=sin2x\)

\(\Leftrightarrow-\dfrac{1}{2}sin2x\left(cosx+sinx\right)=sin2x\)

\(\Leftrightarrow sin2x\left(cosx+sinx+2\right)=0\)

\(\Leftrightarrow sin2x\left[\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\right]=0\)

\(\Leftrightarrow sin2x=0\)

\(\Leftrightarrow x=\dfrac{k\pi}{2}\)

`A=[sin x+sin 2x+sin 3x]/[cos x+cos 2x+cos 3x]`

`A=[(sin x+sin 3x)+sin 2x]/[(cos x+cos 3x)+cos 2x]`

`A=[2sin 2x.cos (-x)+sin 2x]/[2cos 2x.cos (-x)+cos 2x]`

`A=[sin 2x(2cos(-x)+1)]/[cos 2x(2cos(-x)+1)]`

`A=[sin 2x]/[cos 2x]=tan 2x`.