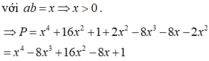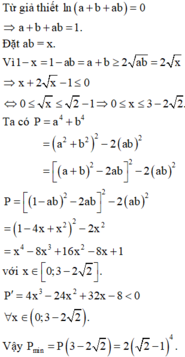CMR : a4 + a3b + ab3 +b4 > hoặc = 0 với mọi a,b thuộc R

Những câu hỏi liên quan
CM: a4+b4≥a3b+ab3 (∀a,b)
\(a^4+b^4-a^3b-ab^3=a^3\left(a-b\right)-b^3\left(a-b\right)=\left(a-b\right)\left(a^3-b^3\right)=\left(a-b\right)\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^2\left(a^2+ab+b^2\right)\)
Có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\a^2+ab+b^2>0\end{matrix}\right.\)
\(\Rightarrow a^4+b^4-a^3b-ab^3\ge0\)
\(\Rightarrow a^4+b^4\ge a^3b+ab^3\)
Đúng 0
Bình luận (0)
Áp dụng BĐT cosi với 2 số không âm:
`a^4+b^4+b^4+b^4>=4\root4{a^4b^12}=4|ab^3|>=4ab^3`
Hoàn toàn tương tự:
`b^4+a^4+a^4+a^4>=4a^3b`
`=>a^4+b^4+b^4+b^4+b^4+a^4+a^4+a^4>=4ab^3+4a^3b`
`<=>4(a^4+b^4)>=4(ab^3+a^3b)`
`<=>a^4+b^4>=ab^3+a^3b`
Đúng 0
Bình luận (0)
b)với a+b+c=0
CMR a4+b4+c4=2(ab+bc+ca)2
theo bài ta có:
a + b + c = 0
=> a = -(b + c)
=> a2 = [-(b + c)]2
=> a2 = b2 + 2bc + c2
=> a2 - b2 - c2 = 2bc
=> ( a2 - b2 - c2)2 = (2bc)2
=> a4 + b4 + c4 - 2a2c2 + 2b2c2 - 2a2c2 = 4b2c2
=> a4 + b4 + c4 = 2a2c2 + 2b2c2 + 2a2c2
=> 2(a4 + b4 + c4) = a4 + b4 + c4 + 2a2c2 + 2b2c2 + 2a2c2
=> 2(a4 + b4 + c4) = (a2 + b2 + c2)2
=> 2(a4 + b4 + c4) = 1
=> a4 + b4 + c4 = \(\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Đề viết sai rồi bạn
Với a+b+c=0
CMR : a4+b4+c4=2(ab+bc+ac)2
Đúng 0
Bình luận (0)
CMR: Với mọi a,b thuộc R thì:
a, a2-4ab+b2 > hoặc = 0
b, -2a2+a-1<0
a:Sửa đề: \(a^2-4ab+4b^2\)
\(=a^2-2\cdot a\cdot2b+4b^2\)
\(=\left(a-2b\right)^2\ge0\)(luôn đúng)
b: \(-2a^2+a-1\)
\(=-2\left(a^2-\dfrac{1}{2}a+\dfrac{1}{2}\right)\)
\(=-2\left(a^2-2\cdot a\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{7}{16}\right)\)
\(=-2\left(a-\dfrac{1}{2}\right)^2-\dfrac{7}{8}\le-\dfrac{7}{8}< 0\forall x\)
Đúng 1
Bình luận (0)
cho a + b + c = 0. Chứng minh đẳng thức:
a) a4 + b4 + c4 = 2(a2b2 + b2c2 +c2a2); b) a4 + b4 + c4 = 2(ab + bc + ca)2;
a4 + b4 + c4 =(a2+b2+c2)2 /2
Cmr nếu a+b=c thì a4 +b4 +c4 = 2a2b2 + 2b2c2 + 2a2c2
Với a,b 0 thỏa mãn điều kiện a + b +ab 1, giá trị nhỏ nhất của
P
a
4
+
b
4
bằng. A. B. C. D.
Đọc tiếp
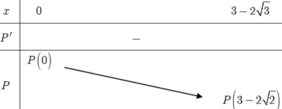
Với a,b > 0 thỏa mãn điều kiện a + b +ab = 1, giá trị nhỏ nhất của P = a 4 + b 4 bằng.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Với a,b 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của
P
a
4
+
b
4
bằng A.
2
+
1
4
.
B.
2
2...
Đọc tiếp
Với a,b > 0 thỏa mãn điều kiện ln(a + b +ab) giá trị nhỏ nhất của P = a 4 + b 4 bằng
A. 2 + 1 4 .
B. 2 2 − 1 4 .
C. 2 − 1 4 .
D. 2 2 + 1 4 .
M= ( a-b) (a^2 + ab + ^2) -(a+b)( a^2 - ab + b^2)
CMR với mọi a thuộc R và b< 0 thì M >0
\(M=\left(a-b\right)\left(a^2+ab+b^2\right)-\left(a-b\right)\left(a^2-ab+b^2\right)\)
\(=\left(a^3-b^3\right)-\left(a^3+b^3\right)\)
\(=-2b^3\)
Lại có : \(b< 0\Leftrightarrow-2b^3>0\)
\(\Leftrightarrow M>0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cho 3 số thực a,b,c thỏa man: a+b+c=3
CMR: a4+b4+c4 ≥ a3+b3+c3
Ta có \(a^4+b^4\ge2a^2.b^2\) (Bất đẳng thức Cô si với \(a^2;b^2\ge0\) )
Tương tự \(b^4+c^4\ge2b^2.c^2;a^4+c^4\ge2a^2.c^2\)
Do đó: \(a^4+b^4+c^4\ge\dfrac{2a^2b^2+2b^2c^2+2a^2c^2}{2}=a^2b^2+b^2c^2+a^2c^2\)(1)
Ta lại có:\(a^2b^2+b^2c^2\ge2ab^2c;b^2c^2+a^2c^2\ge2abc^2;a^2c^2+a^2b^2\ge2a^2bc\)
Nên\(a^2b^2+b^2c^2+a^2c^2\ge a^2bc+ab^2c+abc^2=abc\left(a+b+c\right)=3abc\left(a+b+c=3,gt\right)\)
(1);(2) => \(a^4+b^4+c^4\ge3abc\) ;đẳng thức xảy ra khi a = b = c = 1 (*)
Giả sử: \(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)^3-3ab\left(a+b+c\right)-3c\left(a+b\right)\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left[\left(a+b+c\right)^2-ab-bc-ac\right]\ge0\\2.3\left(a^2+b^2+c^2-ab-bc-ac\right)\ge0\\
\Leftrightarrow3\left(2a^2+2b^2+2c^2-2ab-2bc-2ac\right)\ge0\\\Leftrightarrow3\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\right]\ge0\)
Đúng mới mọi a,b,c ϵR
Vậy \(a^3+b^3+c^3\ge3abc\) và đẳng thức xảy ra khi a=b=c=(a+b+c)/3 =1(**)
Ta lại có \(a^4\ge a^3;b^4\ge b^3;c^4\ge c^3\) mà a+b+c = 3
Nên \(a^4+b^4+c^4>a^3+b^3+c^3\) (***)
Từ (*);(**);(***) ta có điều phải chứng minh và đẳng thức xảy ra khi a= b=c=1
Đúng 0
Bình luận (0)
Tôi có cách chứng minh bằng đồng bậc hóa bất đẳng thức như sau:
ta sẽ chứng minh:
\(3\left(a^4+b^4+c^4\right)>=\left(a+b+c\right)\left(a^3+b^3+c^3\right)\)
<=> \(2\left(a^4+b^4+c^4\right)>=ab\left(a^2+b^2\right)+bc\left(b^2+c^2\right)+ca\left(c^2+a^2\right)\)
mà ta có theo bất đẳng thức AMGM \(a^4+b^4>=\dfrac{\left(a^2+b^2\right)^2}{2}>=\dfrac{2ab\left(a^2+b^2\right)}{2}=ab\left(a^2+b^2\right)\)
làm tương tự rồi cộng lại, ta có đpcm.
Đúng 1
Bình luận (0)