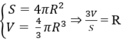Câu 1 : Mặt cầu (S) có bán kính R = \(a\sqrt{2}\) . Tính diện tích của mặt cầu (S)
A. \(8a^2\) B. \(4\Pi a^2\) C. \(8\Pi a^2\) D. \(16\Pi a^2\)
Câu 2 : Công thức tính thể tích khối cầu có bán kính R ?
A. \(\frac{4}{3}\Pi R^2\) B. \(\frac{4}{3}\Pi R^3\) C. \(\frac{1}{3}\Pi R^3\) D. \(\Pi R^3\)
Câu 3 : Một hình hộp chữ nhật có ba kích thước tương ứng là a , 2a , 2a . Tính thể tích khối cầu ngoại tiếp hình hộp
A. \(\frac{9\Pi a^3}{5}\) B. \(\frac{9\Pi a^3}{4}\) C. \(9\Pi a^3\) D. \(\frac{9\Pi a^3}{2}\)
Câu 4 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = \(a\sqrt{3}\) . Cạnh bên SA vuông góc với đáy và SC tạo với đáy 1 góc 600 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
A. Tâm là trung điểm SC , R = 2a
B. Tâm là trung điểm SC , R = 4a
C. Tâm trùng với tâm của đáy , R = a
D. Tâm là trung điểm SD , R = \(\frac{a\sqrt{15}}{2}\)
Câu 5 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với đáy , cạnh bên SB bằng \(a\sqrt{3}\) . Tính thể tích khối cầu ngoại tiếp S.ABCD
A. \(\frac{4}{3}\Pi a^3\) B. \(\frac{16\sqrt{2}}{3}a^3\) C. \(12\sqrt{3}a^3\) D. \(\frac{4}{3}a^3\)
HELP ME !!!!!!!!!!!!!