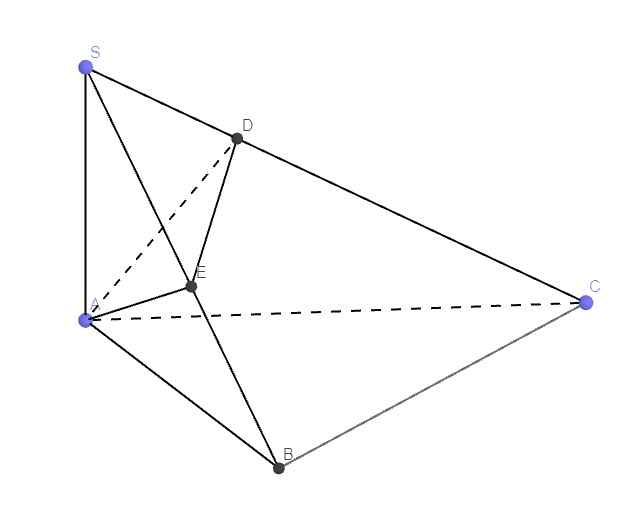
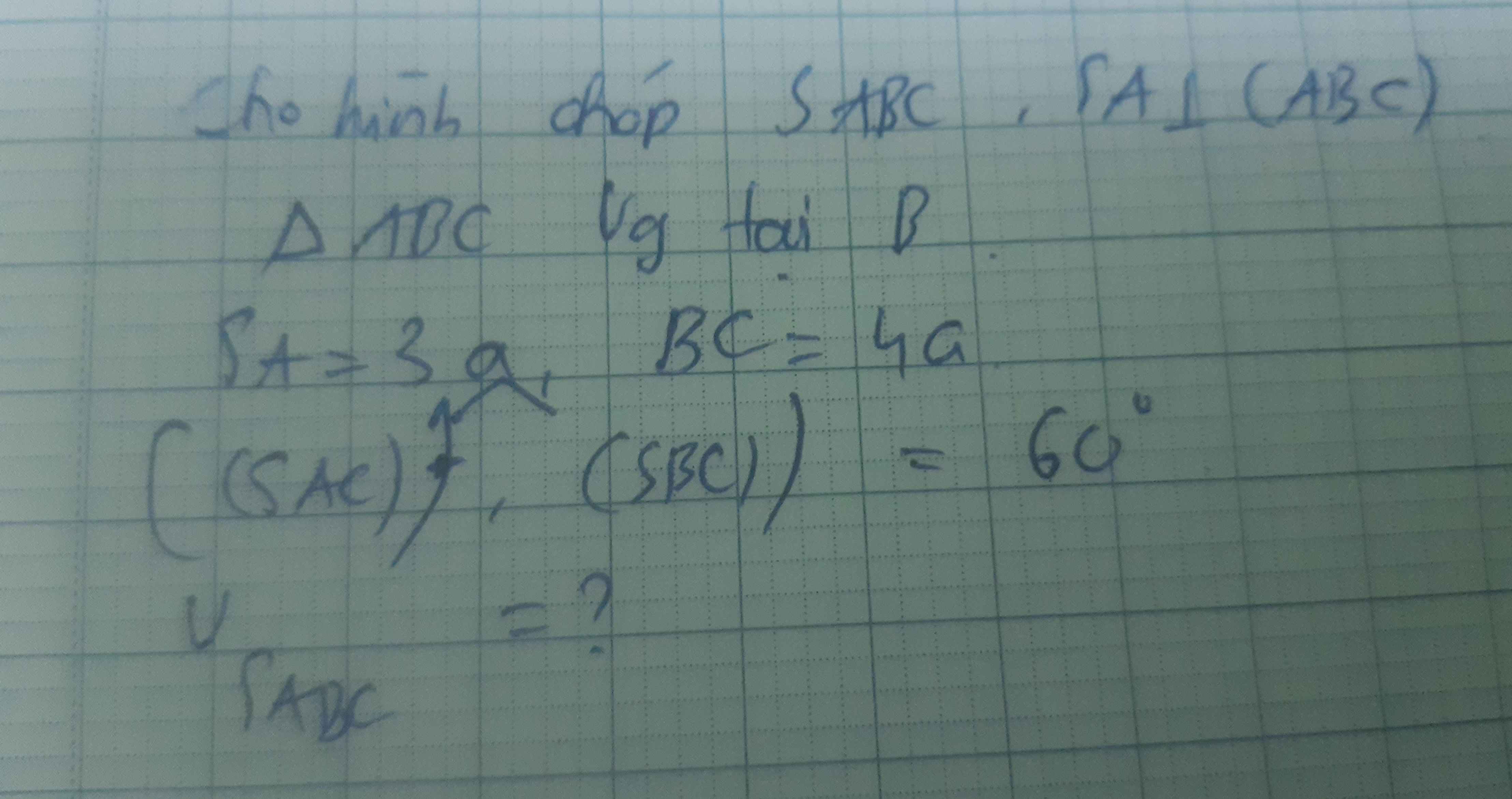Mn vẽ đáy ABC NẰM DƯỚI NHÉ Ạ. MN CHỈ CẦN XÁC ĐỊNH GÓC THÔI
Chuyên đề thể tích 1
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Kẻ \(AE\perp SB\Rightarrow AE\perp\left(SBC\right)\Rightarrow AE\perp SC\)
Kẻ \(AD\perp SC\Rightarrow SC\perp\left(ADE\right)\)
\(\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(\Rightarrow\widehat{ADE}=60^0\)
\(\Rightarrow AE=AD.sin\widehat{ADE}=AD.sin60^0=\dfrac{AD\sqrt{3}}{2}\Rightarrow\dfrac{1}{AE^2}=\dfrac{4}{3AD^2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\) ; \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{4}{3}\left(\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\right)\)
\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{4}{3}.\dfrac{1}{AC^2}+\dfrac{1}{3SA^2}=\dfrac{4}{3}.\dfrac{1}{AB^2+16a^2}+\dfrac{1}{27a^2}\)
Đề có nhầm lẫn đâu không nhỉ, vì phương trình \(\dfrac{1}{x}=\dfrac{4}{3\left(x+16\right)}+\dfrac{1}{27}\) cho nghiệm rất xấu
Đúng 0
Bình luận (0)
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh asqrt{3} . Diện tích xung quanh của hình nón là
A. S_{xq}dfrac{3}{4}πa2 B. S_{xq}dfrac{3sqrt{3}}{8}πa2 C. S_{xq}dfrac{3}{2}πa2 D. S_{xq}dfrac{3sqrt{3}}{4} πa2
Đọc tiếp
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh a\(\sqrt{3}\) . Diện tích xung quanh của hình nón là
A. S\(_{xq}\)=\(\dfrac{3}{4}\)πa2 B. S\(_{xq}\)=\(\dfrac{3\sqrt{3}}{8}\)πa2 C. S\(_{xq}\)=\(\dfrac{3}{2}\)πa2 D. S\(_{xq}\)=\(\dfrac{3\sqrt{3}}{4}\) πa2
Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hai mặt bên (SAB) và (SAD ) cùng vuông góc vs đáy . Góc giữa cạnh bên SC và mặt bên (SAB ) bằng 45° .tính thể tích khối chóp S.ABCD theo a
Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)
Đúng 0
Bình luận (0)
Bài tập 1: Cho hàm số y = \(2x^3\) - 6x - 3 (C).
a, Khảo sát.
b, Viết pTTT của (C) tại giao của (C) với trục tung Oy
a.
\(y'=6x^2-6=0\Rightarrow x=\pm1\)
\(x=-1\) là điểm cực đại của hàm số
\(x=1\) là điểm cực tiểu của hàm số
Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
b. Gọi A là giao điểm của (C) với Oy \(\Rightarrow A\left(0;-3\right)\)
\(f'\left(0\right)=-6\)
Phương trình tiếp tuyến:
\(y=-6\left(x-0\right)-3\Leftrightarrow y=-6x-3\)
Đúng 1
Bình luận (0)
bài1: cho tứ diện OABC có OA1 , OB2 , OC2 . tìm thể tích OABC max
bài 2 : cho hình chóp SABC có đáy là tam giác đều . các cạnh bên cùng bằng 1 và tạo với đáy góc alpha
a. tính thể tích hình chóp theo alpha
b. tìm alpha để thể tích hình chóp lớn nhất
bài 3 : cho hình lăng trụ tam giác đều ABCABC có diện tích tam giác ABC căn 3 và góc tạo bơi mặt phẳng ABC và ABC alpha . tìm thể tích max của lăng trụ
Đọc tiếp
bài1: cho tứ diện OABC có OA=1 , OB=2 , OC=2 . tìm thể tích OABC max
bài 2 : cho hình chóp SABC có đáy là tam giác đều . các cạnh bên cùng bằng 1 và tạo với đáy góc alpha
a. tính thể tích hình chóp theo alpha
b. tìm alpha để thể tích hình chóp lớn nhất
bài 3 : cho hình lăng trụ tam giác đều ABCA'B'C' có diện tích tam giác ABC' = căn 3 và góc tạo bơi mặt phẳng ABC' và ABC = alpha . tìm thể tích max của lăng trụ
Cho hình chóp tam giác S.ABC có cạnh bên SA vuông góc với (ABC). Tam giác ABC là tam giác đều cạnh 3a, 1 mp * (SBC) tạo với (ABC) góc 60°. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tinh thể tích khối chóp A.BCKH
tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật biết chiều dài 36 cm và gấp 4 gấp chiều rộng, chiều cao 8,2.
Cho hình hộp chữ nhật ABCD (ABCD)'. Có abcd là hình vuông cạnh a căn 2 â'=2a tính khoảng cách BD và CD'
Cho hình chóp S.ABC. Điểm M tuỳ ý trên mặt đáy. Mặt phẳng (P) thay đổi qua M cắt các tia SA,SB,SC tại A’,B’,C’. Xác định vị trí của M để thể tích hình chóp S.A’B’C’ nhỏ nhất Giúp mk vs!!! Pleaseee!
Để xác định vị trí của M để thể tích hình chóp S.A'B'C' đạt giá trị lớn nhất, ta sử dụng nguyên lý cơ sở của hình học không gian. Gọi H là trung điểm của đoạn thẳng BC. Ta có: - Đường thẳng A'H song song với đường thẳng BC. - Đường thẳng B'H song song với đường thẳng AC. - Đường thẳng C'H song song với đường thẳng AB. Do đó, ta có thể xem hình chóp S.A'B'C' là hình chóp đồng dạng với hình chóp S.ABC, tức là các cạnh của chúng có tỉ lệ tương ứng. Vì vậy, để thể tích hình chóp S.A'B'C' đạt giá trị lớn nhất, ta cần chọn M sao cho tỉ lệ giữa độ dài các đoạn thẳng SA', SB', SC' và độ dài các đoạn thẳng SA, SB, SC là nhỏ nhất. Đặt x = SA'/SA = SB'/SB = SC'/SC. Ta cần tìm giá trị của x để x đạt giá trị nhỏ nhất. Áp dụng định lí Thales, ta có: x = SA'/SA = S'A'/S'A = MA'/MA. Vì A'H song song với BC, ta có: MA'/MA = A'H/AH = A'C'/AC. Tương tự, ta có: MA'/MA = A'H/AH = A'B'/AB. Do đó, ta có: x = SA'/SA = SB'/SB = SC'/SC = A'C'/AC = A'B'/AB. Vậy, để x đạt giá trị nhỏ nhất, ta cần chọn M sao cho A'C'/AC = A'B'/AB đạt giá trị nhỏ nhất. Từ đó, ta suy ra M nằm trên đường thẳng A'H, với H là trung điểm của đoạn thẳng BC.
Đúng 0
Bình luận (0)