\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)
Pitago tam giác vuông OAH:
\(AH=\sqrt{OA^2-OH^2}=1\)
\(\Rightarrow AB=2AH=2\)
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Điểm A nằm ngoài (S) sao cho OA=5. Tiếp tuyến kẻ từ A tới (S) có tiếp điểm là B. Độ dài AB là
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Qua A kẻ 2 tiếp tuyến từ (S) có tiếp điểm lần lượt là M,N và góc MAN là 60°. Độ dài MN là
cho mặt cầu (S) có tâm O và bán kính R. biết diện tích của (S) là 36π. thể tích của (S) là
cho mặt cầu (s) tâm o và có thể tích là 288π. mặt phẳng (P) cắt (S) tại (C) và khoảng cách từ tâm (S) đến (P) là 2 căn 5 thì bán kính của đường tròn (C) là
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu:
A. h < R
B. h = R
C. h ≤ R
D. h ≥ R
Cho mặt cầu S(O; r), hai mặt phẳng (α) và (β) có khoảng cách đến tâm O của mặt cầu đã cho lần lượt là a và b (0 < a < b < r). Hãy so sánh hai bán kính của các đường tròn giao tuyến.
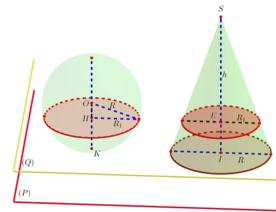
Cho hình cầu tâm O bán kính R , tiếp xúc với mặt phẳng (P) . Một hình nón tròn xoay có đáy nằm trên (P), có chiều cao h = 15 , có bán kính đáy bằng R . Hình cầu và hình nón nằm về một phía đối với mặt phẳng (P) . Người ta cắt hai hình đó bởi mặt phẳng (Q) song song với (P) và thu được hai thiết diện có tổng diện tích là S . Gọi x là khoảng cách giữa (P) và (Q), ( 0 < x ≤ 5 ) . Biết rằng S đạt giá trị lớn nhất khi x = a b (phân số a b tối giản). Tính giá trị T =a+b .
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
A. h ≤ R
B. h ≥ R
C. h > R
D. h < R
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R
