\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(V=\dfrac{4}{3}\pi R^3=36\pi\)
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Hai điểm A,B thuộc (S) và khoảng cách từ O đến AB là 2 căn 2 Tính AB
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Điểm A nằm ngoài (S) sao cho OA=5. Tiếp tuyến kẻ từ A tới (S) có tiếp điểm là B. Độ dài AB là
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Qua A kẻ 2 tiếp tuyến từ (S) có tiếp điểm lần lượt là M,N và góc MAN là 60°. Độ dài MN là
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Thể tích của khối nón theo r và h.
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
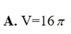
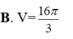
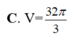
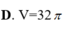
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Xác định h để thể tích của hình nón là lớn nhất.
cho mặt cầu (s) tâm o và có thể tích là 288π. mặt phẳng (P) cắt (S) tại (C) và khoảng cách từ tâm (S) đến (P) là 2 căn 5 thì bán kính của đường tròn (C) là
