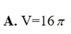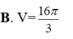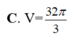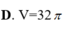ì 0 < a < b < r ⇒
Vậy đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) có bán kính lớn hơn mặt cầu S(O; r) và mặt phẳng (β)
ì 0 < a < b < r ⇒
Vậy đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) có bán kính lớn hơn mặt cầu S(O; r) và mặt phẳng (β)
Cho mặt cầu S(0;R) và mặt phẳng ( α ). Gọi d là khoảng cách từ O tới ( α ). Khi d < R thì mặt phẳng ( α ) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng:
A. R 2 + d 2 B. R 2 - d 2
C. R d d. R 2 - 2 d 2
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Hãy xác định đường tròn giao tuyến của mặt cầu S(O; r) và mặt phẳng (α) biết rằng khoảng cách từ tâm O đến (α) bằng r/2.
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng ( α ) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai?
A. R = r 2 + d 2 ( O , ( α ) )
B. d ( O , ( α ) ) < r
C. Diện tích của mặt cầu là S = 4 πr 2
D. Đường tròn lớn của mặt cầu có bán kính bằng bsn kính mặt cầu.
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).