b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)

\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)

c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)

\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)

\(\Leftrightarrow sin2x\cdot sinx-cos2x\cdot sinx+sin2x\cdot cosx+sinx\cdot cos2x=cosx\left(sinx+cosx\right)\)

=>\(sin2x\left(sinx+cosx\right)=cosx\left(sinx+cosx\right)\)

=>\(\left(sinx+cosx\right)\cdot\left(sin2x-cosx\right)=0\)

=>\(cosx\cdot\left(2sinx-1\right)\cdot\sqrt{2}\cdot sin\left(x+\dfrac{pi}{4}\right)=0\)

=>\(\left[{}\begin{matrix}cosx=0\\2sinx-1=0\\sin\left(x+\dfrac{pi}{4}\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\sinx=\dfrac{1}{2}\\x+\dfrac{pi}{4}=kpi\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\x=-\dfrac{pi}{4}+kpi\\sinx=\dfrac{1}{2}\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{pi}{2}+kpi\\x=-\dfrac{pi}{4}+kpi\\x=\dfrac{pi}{6}+k2pi\\x=\dfrac{5}{6}pi+k2pi\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{pi}{2}+kpi;-\dfrac{pi}{4}+kpi;\dfrac{pi}{6}+k2pi;\dfrac{5}{6}pi+k2pi\right\}\)

a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)

\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)

\(=3sinx-4sin^3x\)

b/

\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)

\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)

\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)

c/

\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)

\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)

d/

\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)

e/

a/

\(\sqrt{3}sin4x-cos4x=2cosx\)

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin4x-\frac{1}{2}cos4x=cosx\)

\(\Leftrightarrow sin\left(4x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{2}-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-\frac{\pi}{6}=\frac{\pi}{2}-x+k2\pi\\4x-\frac{\pi}{6}=\frac{\pi}{2}+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2\pi}{15}+\frac{k2\pi}{5}\\x=\frac{2\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)

b/

\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x-\sqrt{3}cos2x\)

\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)

\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=sin\left(2x-\frac{\pi}{3}\right)\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(\frac{\pi}{6}-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}-x+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow cos3x-\sqrt{3}sin3x=\sqrt{3}cos2x-sin2x\)

\(\Leftrightarrow\frac{1}{2}cos3x-\frac{\sqrt{3}}{2}sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)

\(\Leftrightarrow cos\left(3x+\frac{\pi}{3}\right)=cos\left(2x+\frac{\pi}{6}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\3x+\frac{\pi}{3}=-2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=-\frac{\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)

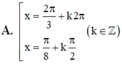
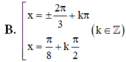
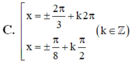
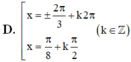
Chọn D

Ta sẽ biến đổi phương trình thành dạng tích

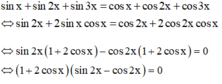
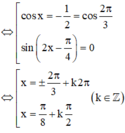
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

`A=[sin x+sin 2x+sin 3x]/[cos x+cos 2x+cos 3x]`

`A=[(sin x+sin 3x)+sin 2x]/[(cos x+cos 3x)+cos 2x]`

`A=[2sin 2x.cos (-x)+sin 2x]/[2cos 2x.cos (-x)+cos 2x]`

`A=[sin 2x(2cos(-x)+1)]/[cos 2x(2cos(-x)+1)]`

`A=[sin 2x]/[cos 2x]=tan 2x`.