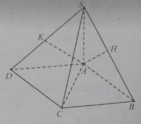
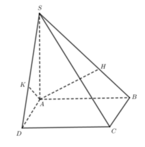
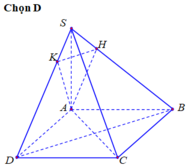
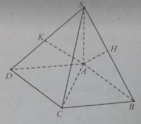
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với mặt đáy . Dựng AH , AK , AM lần lượt là các đường cao trong các tam giác SAB , SAD , SAC
1)CMR: AH vuông góc với SC , AK vuông góc với SC . Chứng tỏ AH , AK , AM đồng phẳng
2)CMR: KH vuông góc với AM