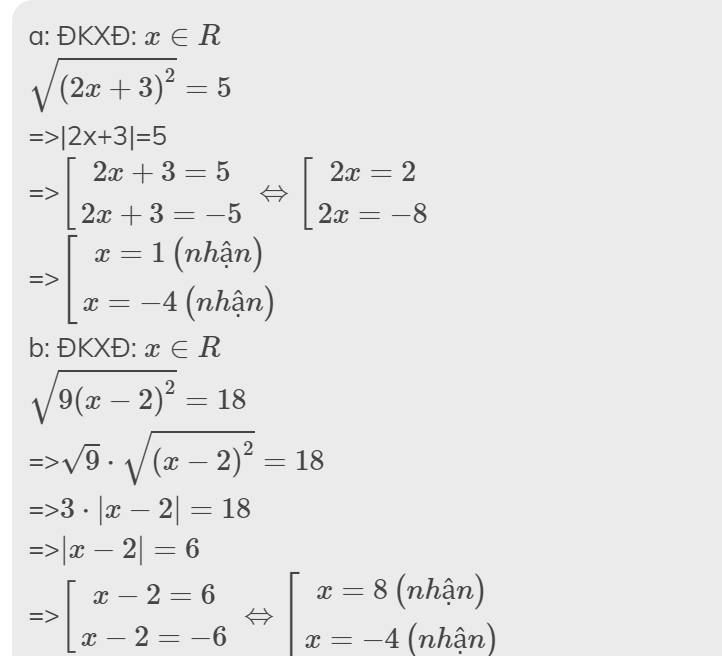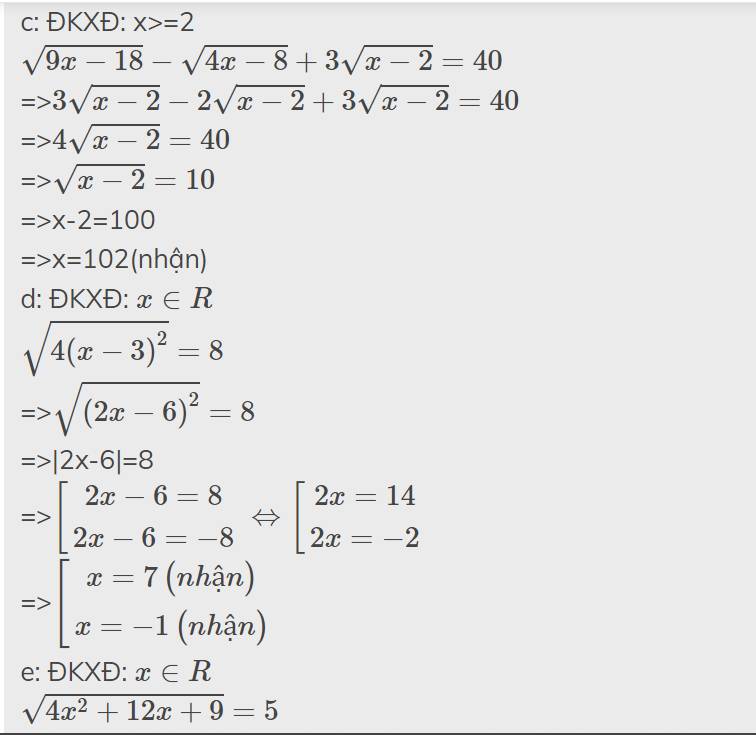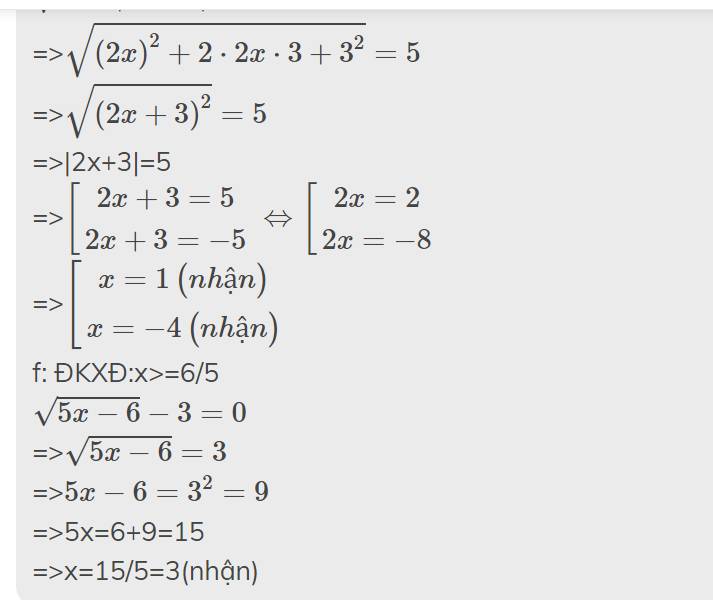a: \(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\cdot3\sqrt{x-2}+6\cdot\dfrac{\sqrt{x-2}}{9}=-4\)

\(\Leftrightarrow\sqrt{x-2}=4\)

=>x-2=16

hay x=18

b: \(\Leftrightarrow\left|3x+2\right|=4x\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+2=4x\left(x>=-\dfrac{2}{3}\right)\\3x+2=-4x\left(x< -\dfrac{2}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-\dfrac{2}{7}\left(nhận\right)\end{matrix}\right.\)

c: \(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)

\(\Leftrightarrow4\sqrt{x-2}=40\)

=>x-2=100

hay x=102

d: =>5x-6=9

hay x=3

\(a,\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\left(dk:x\ge2\right)\)

\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)

\(\Leftrightarrow\sqrt{x-2}=4\)

\(\Leftrightarrow x-2=16\)

\(\Leftrightarrow x=18\left(tmdk\right)\)

b,\(\sqrt{9x^2-12x+4=3x\left(dk:x\ge0\right)}\)

\(\Leftrightarrow\sqrt{\left(3x-2\right)^2}=3x\)

\(\Leftrightarrow\left|3x-2\right|=3x\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x-2=3x\\3x-2=-3x\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x\in\varnothing\\x=\dfrac{1}{3}\left(tmdk\right)\end{matrix}\right.\)

Các câu còn lại làm tương tự nhé 

\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: x≥2)

\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+6\sqrt{\dfrac{1}{81}\left(x-2\right)}=-4\)

\(\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)

\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{4}{3}\sqrt{x-2}=-4\)

\(-\sqrt{x-2}=-4\)

\(\sqrt{x-2}=4\)

\(\left|x-2\right|=16\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=16\\x-2=-16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=18\left(TM\right)\\x=-14\left(L\right)\end{matrix}\right.\)

a) Ta có: \(\sqrt{25x+75}+2\sqrt{9x+27}=5\sqrt{x+3}+18\)

\(\Leftrightarrow5\sqrt{x+3}+6\sqrt{x+3}-5\sqrt{x+3}=18\)

\(\Leftrightarrow\sqrt{x+3}=3\)

\(\Leftrightarrow x+3=9\)

hay x=6

b) Ta có: \(\sqrt{4x-8}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)

\(\Leftrightarrow2\sqrt{x-2}-2\sqrt{x-2}-3\sqrt{x-2}=8\)

\(\Leftrightarrow-3\sqrt{x-2}=8\)(Vô lý)

a: ĐKXĐ: \(x\in R\)

\(\sqrt{\left(2x+3\right)^2}=5\)

=>|2x+3|=5

=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)

b: ĐKXĐ: \(x\in R\)

\(\sqrt{9\left(x-2\right)^2}=18\)

=>\(\sqrt{9}\cdot\sqrt{\left(x-2\right)^2}=18\)

=>\(3\cdot\left|x-2\right|=18\)

=>\(\left|x-2\right|=6\)

=>\(\left[{}\begin{matrix}x-2=6\\x-2=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: x>=2

\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)

=>\(3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)

=>\(4\sqrt{x-2}=40\)

=>\(\sqrt{x-2}=10\)

=>x-2=100

=>x=102(nhận)

d: ĐKXĐ: \(x\in R\)

\(\sqrt{4\left(x-3\right)^2}=8\)

=>\(\sqrt{\left(2x-6\right)^2}=8\)

=>|2x-6|=8

=>\(\left[{}\begin{matrix}2x-6=8\\2x-6=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=14\\2x=-2\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

e: ĐKXĐ: \(x\in R\)

\(\sqrt{4x^2+12x+9}=5\)

=>\(\sqrt{\left(2x\right)^2+2\cdot2x\cdot3+3^2}=5\)

=>\(\sqrt{\left(2x+3\right)^2}=5\)

=>|2x+3|=5

=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)

f: ĐKXĐ:x>=6/5

\(\sqrt{5x-6}-3=0\)

=>\(\sqrt{5x-6}=3\)

=>\(5x-6=3^2=9\)

=>5x=6+9=15

=>x=15/5=3(nhận)

ĐKXĐ: x>=2

\(\sqrt{9x-18}+5\sqrt{4x-8}=\sqrt{x-2}+3\)

=>\(3\sqrt{x-2}+10\sqrt{x-2}-\sqrt{x-2}=3\)

=>\(12\sqrt{x-2}=3\)

=>\(\sqrt{x-2}=\dfrac{1}{4}\)

=>x-2=1/16

=>x=33/16

`a)sqrt{5x-2}=3(x>=2/5)`

`<=>5x-2=9`

`<=>5x=11`

`<=>x=11/5(tm)`

`b)sqrt{x^2-4x+4}-5=0`

`<=>\sqrt{(x-2)^2}=5`

`<=>|x-2|=5`

`<=>` \(\left[ \begin{array}{l}x-2=5\\x-2=-5\end{array} \right.\) 

`<=>` \(\left[ \begin{array}{l}x=7\\x=-3\end{array} \right.\) 

`c)3sqrt{4x+8}-sqrt{9x+18}+9sqrt{(x+2)/9}=sqrt{72}(x>=-2)`

`<=>6sqrt{x+2}-3sqrt{x+2}+3sqrt{x+2}=sqrt{72}`

`<=>6sqrt{x+2}=6sqrt2`

`<=>sqrt{x+2}=sqrt2`

`<=>x+2=2`

`<=>x=0(tm)`

\(a,ĐK:x\ge\dfrac{2}{5}\)

\(\Leftrightarrow5x-2=9\)

\(\Leftrightarrow5x=11\)

\(\Leftrightarrow x=\dfrac{11}{5}\)

\(b,\)

\(\Leftrightarrow x^2-5x+4=25\)

\(\Leftrightarrow x^2-5x-21=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{109}}{2}\\x=\dfrac{5-\sqrt{109}}{2}\end{matrix}\right.\)

\(c,\)

\(\Leftrightarrow6\sqrt{x+2}-3\sqrt{x+2}+9\cdot\sqrt{\dfrac{x+2}{9}}=6\sqrt{2}\)

\(\Leftrightarrow2\sqrt{x+2}-\sqrt{x+2}+3\cdot\sqrt{\dfrac{x+2}{9}}=2\sqrt{2}\)

Đặt \(\sqrt{x+2}=a\) ta có (1)

\(2a-a+3\cdot\dfrac{a}{\sqrt{9}}=2\sqrt{2}\)

\(\Leftrightarrow a+3\cdot\dfrac{a}{3}=2\sqrt{2}\)

\(\Leftrightarrow2a=2\sqrt{2}\)

\(\Leftrightarrow a=\sqrt{2}\)

Thay \(a=\sqrt{2}\) vào (1) ta có

\(\sqrt{x+2}=\sqrt{2}\)

\(\Leftrightarrow x+2=2\)

\(\Leftrightarrow x=0\)

a) Ta có: \(\sqrt{25x+75}+3\sqrt{x-2}=2\sqrt{x-2}+\sqrt{9x-18}\)

\(\Leftrightarrow5\sqrt{x+3}+3\sqrt{x-2}=2\sqrt{x-2}+3\sqrt{x-2}\)

\(\Leftrightarrow\sqrt{25x+75}=\sqrt{4x-8}\)

\(\Leftrightarrow25x-4x=-8-75\)

\(\Leftrightarrow21x=-83\)

hay \(x=-\dfrac{83}{21}\)

b) Ta có: \(\sqrt{\left(2x-1\right)^2}=4\)

\(\Leftrightarrow\left|2x-1\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

c) Ta có: \(\sqrt{\left(2x+1\right)^2}=3x-5\)

\(\Leftrightarrow\left|2x+1\right|=3x-5\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=3x-5\left(x\ge-\dfrac{1}{2}\right)\\2x+1=5-3x\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3x=-5-1\\2x+3x=5-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\left(nhận\right)\\x=\dfrac{4}{5}\left(loại\right)\end{matrix}\right.\)

d) Ta có: \(\sqrt{4x-12}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)

\(\Leftrightarrow2\sqrt{x-3}-2\sqrt{x-2}=3\sqrt{x-2}+8\)

\(\Leftrightarrow2\sqrt{x-3}-5\sqrt{x-2}=8\)

\(\Leftrightarrow4\left(x-3\right)+25\left(x-2\right)-20\sqrt{x^2-5x+6}=8\)

\(\Leftrightarrow4x-12+25x-50-8=20\sqrt{\left(x-2\right)\left(x-3\right)}\)

\(\Leftrightarrow20\sqrt{\left(x-2\right)\left(x-3\right)}=29x-70\)

\(\Leftrightarrow x^2-5x+6=\dfrac{\left(29x-70\right)^2}{400}\)

\(\Leftrightarrow x^2-5x+6=\dfrac{841}{400}x^2-\dfrac{203}{20}x+\dfrac{49}{4}\)

\(\Leftrightarrow\dfrac{-441}{400}x^2+\dfrac{103}{20}x-\dfrac{25}{4}=0\)

\(\Delta=\left(\dfrac{103}{20}\right)^2-4\cdot\dfrac{-441}{400}\cdot\dfrac{-25}{4}=-\dfrac{26}{25}\)(Vô lý)

vậy: Phương trình vô nghiệm

b: ĐKXĐ: x>=2

\(2\sqrt{9x-18}-\sqrt{x-2}+\dfrac{1}{2}\cdot\sqrt{4x-8}=18\)

=>\(2\cdot3\cdot\sqrt{x-2}-\sqrt{x-2}+\dfrac{1}{2}\cdot2\sqrt{x-2}=18\)

=>\(6\sqrt{x-2}=18\)

=>\(\sqrt{x-2}=3\)

=>x-2=9

=>x=11(nhận)

c: Ta có: \(\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\)

\(\Leftrightarrow2\sqrt{x-1}=4\)

\(\Leftrightarrow x-1=4\)

hay x=5

e: Ta có: \(\sqrt{4x^2-28x+49}-5=0\)

\(\Leftrightarrow\left|2x-7\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-7=5\\2x-7=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)

a. ĐKXĐ: $x\in\mathbb{R}$

PT $\Leftrightarrow \sqrt{(x-2)^2}=2-x$

$\Leftrightarrow |x-2|=2-x$
$\Leftrightarrow 2-x\geq 0$

$\Leftrightarrow x\leq 2$

b. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \sqrt{4}.\sqrt{x-2}-\frac{1}{5}\sqrt{25}.\sqrt{x-2}=3\sqrt{x-2}-1$

$\Leftrightarrow 2\sqrt{x-2}-\sqrt{x-2}=3\sqrt{x-2}-1$

$\Leftrightarrow 1=2\sqrt{x-2}$

$\Leftrightarrow \frac{1}{2}=\sqrt{x-2}$

$\Leftrightarrow \frac{1}{4}=x-2$

$\Leftrightarrow x=\frac{9}{4}$ (tm)

c. ĐKXĐ: $x\geq 1$

PT $\Leftrightarrow \sqrt{x-1}+\sqrt{9}.\sqrt{x-1}-\sqrt{4}.\sqrt{x-1}=4$

$\Leftrightarrow \sqrt{x-1}+3\sqrt{x-1}-2\sqrt{x-1}=4$

$\Leftrightarrow 2\sqrt{x-1}=4$

$\Leftrightarrow \sqrt{x-1}=2$

$\Leftrightarrow x-1=4$

$\Leftrightarrow x=5$ (tm)

d. ĐKXĐ: $x\geq 2$

PT $\Leftrightarrow \frac{1}{2}\sqrt{x-2}-4\sqrt{\frac{4}{9}}\sqrt{x-2}+\sqrt{9}.\sqrt{x-2}-5=0$

$\Leftrightarrow \frac{1}{2}\sqrt{x-2}-\frac{8}{3}\sqrt{x-2}+3\sqrt{x-2}-5=0$

$\Leftrightarrow \frac{5}{6}\sqrt{x-2}-5=0$

$\Leftrightarrow \sqrt{x-2}=6$

$\Leftrightarrow x-2=36$

$\Leftrightarrow x=38$ (tm)