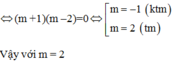cho pt: x3-3mx2-3x+3m+2=0. Tìm m để pt có 3 nghiệm phân biệt thỏa mãn x12+x22+x32>15

Những câu hỏi liên quan
Cho hàm số y=(x-1)(x2+mx+m)
a. Với m=2, tính y', giải pt
b.Tìm m để tiếp tuyến tại điểm có hoành độ x=-1 song song với đường thẳng y=-2x-3
c. tìm m để pt y=0 có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x12 + x22 +x32 <4
d. tìm m để pt y=0 có 3 nghiệm phân biệt trong đó có 1 nghiệm lớn hơn 2
Tìm m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
3
m
x
-
1
cắt trục Ox tại 3 điểm phân biệt có hoành độ
x
1
;
x
2
;
x
3
thỏa điều kiện
x
1
2
+...
Đọc tiếp
Tìm m để đồ thị hàm số y = x 3 - 3 m x 2 + 3 m x - 1 cắt trục Ox tại 3 điểm phân biệt có hoành độ x 1 ; x 2 ; x 3 thỏa điều kiện x 1 2 + x 2 2 + x 3 2 > 15
A. m ∈ - ∞ ; - 1 3 ∪ 1 ; + ∞
B. m ∈ - ∞ ; - 1 ∪ 1 ; + ∞
C. m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
D. m ∈ - ∞ ; - 1 3 ∪ 5 3 ; + ∞
Hoành độ giao điểm của (C) và Ox là nghiệm phương trình
x - 1 x 2 - 3 m - 1 x + 1 = 0 ⇔ x = 1 g x = x 2 - 3 m - 1 x + 1 = 0 1
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt thì (1) có 2 nghiệm phân biệt khác 1.
Khi đó ∆ > 0 g 1 ≠ 0
⇔ m > 1 m < - 1 3 m ≠ 1 ⇔ m > 1 m < - 1 3
Giả sử x 3 = 1
Theo đề thì phương trình (1) có hai nghiệm x 1 ; x 2
x 1 2 + x 2 2 > 14 ⇔ x 1 + x 2 2 - 2 x 1 x 2 > 14 ⇔ m > 5 3 m < - 1
(thỏa mãn)
Vậy m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
Đáp án C
Đúng 0
Bình luận (0)
Cho phương trình: x3- 5x2 + (2m+5)x-4m+2 = 0 (m là tham số )
a) Tìm đk của m để pt có 3 nghiệm phân biệt x1,x2,x3
b) Tìm gt của m để x12 + x22 + x32 = 11
\(x^3-5x^2+2mx+5x-4m+2=0\)
\(\Leftrightarrow\left(x^3-5x^2+5x+2\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x-1\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-3x+2m-1=0\left(1\right)\end{matrix}\right.\)
a. Pt đã cho có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb khác 2
\(\Leftrightarrow\left\{{}\begin{matrix}4-6+2m-1\ne0\\\Delta=9-4\left(2m-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m< \dfrac{13}{8}\end{matrix}\right.\)
b. Do vai trò 3 nghiệm như nhau, không mất tính tổng quát, giả sử \(x_1;x_2\) là nghiệm của (1) và \(x_3=2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2+x_3^2=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+4=11\)
\(\Leftrightarrow9-2\left(2m-1\right)-7=0\)
\(\Leftrightarrow m=1\)
Đúng 2
Bình luận (0)
cho pt x2 - 2(m+1)x + m2 - 1=0. Tìm để phương trình có hai nghiệm phân biệt thỏa mãn x12 + x22 = x1x2 +8
\(\Delta'=\left[-\left(m+1\right)^2\right]-\left(m^2-1\right)\\ =m^2+2m+1-m^2+1\\ =2m+2\)
Để PT có 2 nghiệm phân biệt thì: \(\Delta'>0\)
\(\Leftrightarrow2m+2>0\\\Leftrightarrow2m>-2\\ \Leftrightarrow m>-1 \)
Theo vi ét có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{2\left(m+1\right)}{1}=2m+2\\x_1x_2=\dfrac{c}{a}=m^2-1\end{matrix}\right.\)
Theo đề có:
\(x_1^2+x_2^2=x_1x_2+8\\ \Leftrightarrow x_1^2+x_2^2-x_1x_2-8=0\\ \Leftrightarrow x_1^2+x_2^2+2x_1x_2-x_1x_2-2x_1x_2-8=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2-8=0\\ \Leftrightarrow\left(2m+2\right)^2-3\left(m^2-1\right)-8=0\\ \Leftrightarrow4m^2+8m+4-3m^2+3-8\\ \Leftrightarrow m^2+8m-1=0 \)
\(\Delta=8^2-4.-1=64+4=68\) > 0
\(\Rightarrow m_1=\dfrac{-8+\sqrt{68}}{2}=-4+\sqrt{17}\left(nhận\right)\)
\(m_2=\dfrac{-8-\sqrt{68}}{2}=-4-\sqrt{17}\left(loại\right)\)
Vậy để phương trình có hai nghiệm phân biệt thỏa mãn x12 + x22 = x1x2 +8 thì m có giá trị là \(-4+\sqrt{17}\)
$HaNa$
Đúng 1
Bình luận (0)
Δ=(2m+2)^2-4(m^2-1)
=4m^2+8m+4-4m^2+4=8m+8
Để phương trình có hai nghiệm phân biệt thì 8m+8>0
=>m>-1
x1^2+x2^2=x1x2+8
=>(x1+x2)^2-2x1x2-x1x2=8
=>(2m+2)^2-3(m^2-1)-8=0
=>4m^2+8m+4-3m^2+3-8=0
=>m^2+8m-1=0
=>m=-4+căn 17(nhận) hoặc m=-4-căn 17(loại)
Đúng 1
Bình luận (0)
Cho phương trình: x2 - 3x - m2 + m + 2 = 0 (1)
Tìm m để pt(1) có 2 nghiệm phân biệt x1,x2 sao cho: x12 + x22 = 5
\(\Delta=9-4\left(-m^2+m+2\right)=4m^2-4m+1=\left(2m-1\right)^2\)
Pt có 2 nghiệm pb khi \(m\ne\dfrac{1}{2}\)
Do vai trò của 2 nghiệm là như nhau, giả sử: \(\left\{{}\begin{matrix}x_1=\dfrac{3-\left(2m-1\right)}{2}=2-m\\x_2=\dfrac{3+2m-1}{2}=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\Leftrightarrow\left(2-m\right)^2+\left(m+1\right)^2=5\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình:
x
2
– 2(m – 1)x +
m
2
− 3m 0. Tìm m để phương trình có 2 nghiệm phân biệt
x
1
;
x
2
thỏa mãn
x
1
2
+
x
2
2
8
A. m 2 B....
Đọc tiếp
Cho phương trình: x 2 – 2(m – 1)x + m 2 − 3m = 0. Tìm m để phương trình có 2 nghiệm phân biệt x 1 ; x 2 thỏa mãn x 1 2 + x 2 2 = 8
A. m = 2
B. m = −1
C. m = −2
D. m = 1
Cho phương trình x2 – 5x + 3m + 1 = 0 (m là tham số). Tìm tất cả các giá trị của m để phương trình trên có hai nghiệm phân biệt x1, x2 thỏa mãn | x 1 2 − x 2 2 | = 15
Phương trình có hai nghiệm phân biệt x1, x2 ⇔ ∆ = 52 – 4(3m + 1) > 0 ⇔ 21 – 12m > 0
ó m < 21/12
Với m < 21/12 , ta có hệ thức x 1 + x 2 = 5 x 1 x 2 = 3 m + 1 V i e t '
⇒ | x 1 − x 2 | = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = 5 2 − 4 ( 3 m + 1 ) = 21 − 12 m = > | x 1 2 − x 2 2 | = | ( x 1 + x 2 ) ( x 1 − x 2 ) | = | 5 ( x 1 − x 2 ) | = 5 | x 1 − x 2 | = 5 21 − 12 m
Ta có: | x 1 2 − x 2 2 | = 15 ⇔ 5 21 − 12 m = 15 ⇔ 21 − 12 m = 3 ⇔ 21 − 12 m = 9 ⇔ 12 m = 12 ⇔ m = 1 (t/m)
Vậy m = 1 là giá trị cần tìm
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
+
2
m
+
2
x
2
+
8
−
5
m
x
+
m
−
5
có đồ thị
C
m
và đường thẳng
d
:
y...
Đọc tiếp
Cho hàm số y = x 3 + 2 m + 2 x 2 + 8 − 5 m x + m − 5 có đồ thị C m và đường thẳng d : y = x − m + 1 . Tìm số các giá trị của m để d cắt C m tại 3 điểm phân biệt có hoành độ tại x 1 , x 2 , x 3 thỏa mãn x 1 2 + x 2 2 + x 3 2 = 20.
A. 2
B. 1
C. 3
D. 0
Đáp án A
Phương trình hoành độ giao điểm
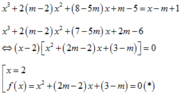
Để phương trình có 3 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 2
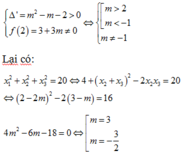
Vậy có 2 giá trị của m thỏa mãn.
Đúng 0
Bình luận (0)
Cho đồ thị
C
m
:
y
x
3
-
2
x
2
+
1
-
m
x
+
m
. Tất cả giá trị của tham số m để
C
m
cắt trục hoành tại ba điểm phân biệt có hoành độ
x...
Đọc tiếp
Cho đồ thị C m : y = x 3 - 2 x 2 + 1 - m x + m . Tất cả giá trị của tham số m để C m cắt trục hoành tại ba điểm phân biệt có hoành độ x 1 , x 2 , x 3 thỏa mãn x 1 2 + x 2 2 + x 3 2 = 4 là
A. m = 1
B. m ≠ 0
C. m = 2
D. m > - 1 4 v à m ≠ 0
Bài 6: Cho PT x² + mx + m+30.c) Giải PT khi m -2. d) Tìm m để PT có hai nghiệm phân biệt x, ,x, thỏa mãn x +x 9. e) Tim m để PT có hai nghiệm phân biệt x, r, thỏa mãn 2x, +3x, 5. f) Tìm m để PT có nghiệm x, -3. Tính nghiệm còn lại. g) Tìm biểu thúức liên hệ giữa hai nghiệm phân biệt x,,x, không phụ thuộc vào m. GIÚP MÌNH GẤP VỚI Ạ MÌNH ĐANG CẦN GẤP ;
Đọc tiếp
Bài 6: Cho PT x² + mx + m+3=0.
c) Giải PT khi m -2.
d) Tìm m để PT có hai nghiệm phân biệt x, ,x, thỏa mãn x +x =9.
e) Tim m để PT có hai nghiệm phân biệt x, r, thỏa mãn 2x, +3x, = 5.
f) Tìm m để PT có nghiệm x, =-3. Tính nghiệm còn lại.
g) Tìm biểu thúức liên hệ giữa hai nghiệm phân biệt x,,x, không phụ thuộc vào m.
GIÚP MÌNH GẤP VỚI Ạ MÌNH ĐANG CẦN GẤP ;<
c: Thay m=-2 vào pt, ta được:
\(x^2-2x+1=0\)
hay x=1
f: Thay x=-3 vào pt, ta được:
\(9-3m+m+3=0\)
=>-2m+12=0
hay m=6
Đúng 1
Bình luận (0)