Cho tam giác ABC đều có AB = 2a. Gọi I là trung điểm của trung tuyến AM. Tính \(\left|\overrightarrow{BA}-\overrightarrow{BI}\right|\) theo a.

Những câu hỏi liên quan
Cho tam giác đều ABC, AB 2a. Gọi M là trung điểm của cạnh BC.
a, Chứng minh rằng: overrightarrow{AB}+overrightarrow{MB}+overrightarrow{MA}overrightarrow{0}
b, Tính left|overrightarrow{AM}+overrightarrow{AC}right| theo a?
c, Tìm vị trí điểm N thỏa mãn: 3overrightarrow{NA}+3overrightarrow{NB}+2overrightarrow{NC}overrightarrow{0}
Đọc tiếp
Cho tam giác đều ABC, AB = 2a. Gọi M là trung điểm của cạnh BC.
a, Chứng minh rằng: \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)
b, Tính \(\left|\overrightarrow{AM}+\overrightarrow{AC}\right|\) theo a?
c, Tìm vị trí điểm N thỏa mãn: \(3\overrightarrow{NA}+3\overrightarrow{NB}+2\overrightarrow{NC}=\overrightarrow{0}\)
Có vẻ không đúng.
Giả sử \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow M\equiv B\) (Vô lí)
Đúng 0
Bình luận (3)
Hình vẽ:
a, Chứng minh \(\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{MA}=\overrightarrow{0}\)
Ta có \(\overrightarrow{AB}+\overrightarrow{BM}+\overrightarrow{MA}=\overrightarrow{BM}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{BM}+\overrightarrow{MB}=\overrightarrow{0}\)
b, Gọi H là trung điểm \(MC\)
Ta có \(AM=\sqrt{AC^2-MC^2}=\sqrt{4a^2-a^2}=a\sqrt{3}\)
\(AH=\sqrt{AM^2+MH^2}=\sqrt{\left(a\sqrt{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=a.\dfrac{\sqrt{13}}{2}\)
\(\left|\overrightarrow{AM}+\overrightarrow{AC}\right|=\left|2\overrightarrow{AH}\right|=2AH=a\sqrt{13}\)
c, Gọi D là trung điểm AB
\(3\overrightarrow{NA}+3\overrightarrow{NB}+2\overrightarrow{NC}=3\left(\overrightarrow{NA}+\overrightarrow{NB}\right)+2\overrightarrow{NC}=6\overrightarrow{ND}+2\overrightarrow{NC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{NC}=3\overrightarrow{DN}\)
Vậy N thuộc đoạn CD sao cho \(CN=\dfrac{3}{4}CD\)
Đúng 1
Bình luận (0)
1) Cho tam giác ABC đều cạnh 5. M là trung điểm BC. I là trung điểm AM. Tính left|overrightarrow{BI}+overrightarrow{CI}right|2) Cho tam giác ABC đều cạnh 7. G là trọng tâm. M là trung điểm AB. Tính left|overrightarrow{AG}+overrightarrow{AM}right|3) Cho ngũ giác đều ABCDE nội tiếp (O). Tính overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}+overrightarrow{OD}+overrightarrow{OE}
Đọc tiếp
1) Cho tam giác ABC đều cạnh 5. M là trung điểm BC. I là trung điểm AM. Tính \(\left|\overrightarrow{BI}+\overrightarrow{CI}\right|\)
2) Cho tam giác ABC đều cạnh 7. G là trọng tâm. M là trung điểm AB. Tính \(\left|\overrightarrow{AG}+\overrightarrow{AM}\right|\)
3) Cho ngũ giác đều ABCDE nội tiếp (O). Tính \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}\)
Cho tam giác ABC có trọng tâm G, gọi I là trung điểm BC. Tìm tập hợp điểm M thỏa mãn: \(2\left|\overrightarrow{MC}+\overrightarrow{IA}-\overrightarrow{IM}-\overrightarrow{BM}\right|=3\left|\overrightarrow{AB}+\overrightarrow{MC}-\overrightarrow{AM}\right|\)
Gt ⇒ \(2\left|\overrightarrow{MC}+\overrightarrow{MA}+\overrightarrow{MB}\right|=3\left|\overrightarrow{MB}+\overrightarrow{MC}\right|\)
Do G là trọng tâm của ΔABC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\)
⇒ VT = 6MG
I là trung điểm của BC
⇒ \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\)
⇒ VP = 6MI
Khi VT = VP thì MG = MI
Vậy tập hợp các điểm M thỏa mãn ycbt là đường trung trực của đoạn thẳng IG
Đúng 3
Bình luận (0)
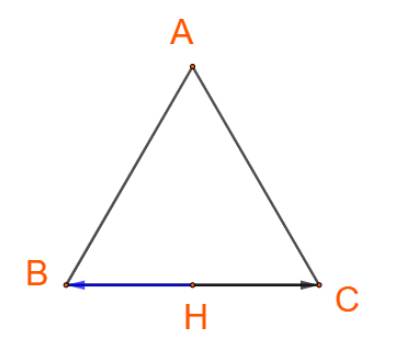
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)

+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
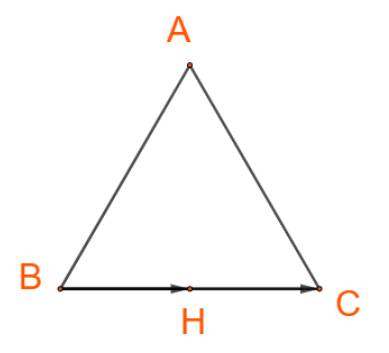
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
Đúng 0
Bình luận (0)
1.Cho hình vuông ABCD cạnh a . Tính left|overrightarrow{AD}+overrightarrow{3AB}right| theo a 2. Cho tam giác ABC đều cạnh a. M là trung điểm BC . Tính left|overrightarrow{MA}+3overrightarrow{MB}+overrightarrow{MC}right|theo a 3. Cho tam giác ABC đều cạnh a có G là trọng tâm . Tính left|overrightarrow{AB}-overrightarrow{GC}right|theo aGiups mik vs ạ . Tks
Đọc tiếp
1.Cho hình vuông ABCD cạnh a . Tính \(\left|\overrightarrow{AD}+\overrightarrow{3AB}\right|\) theo a
2. Cho tam giác ABC đều cạnh a. M là trung điểm BC . Tính \(\left|\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC}\right|\)theo a
3. Cho tam giác ABC đều cạnh a có G là trọng tâm . Tính \(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|\)theo a
Giups mik vs ạ . Tks
1.
Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)
\(=AD^2+9AB^2=10AB^2=10a^2\)
\(\Rightarrow P=a\sqrt{10}\)
2.
Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)
\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)
\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)
\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)
\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)
Đúng 2
Bình luận (0)
1. Cho tam giác ABC có O là điểm thỏa mãn overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}overrightarrow{0} và OAOBOC. Gọi M ,N ll là trung điểm của BC,AC . Tính số đo của left(overrightarrow{AM,}overrightarrow{BN}right)2. Cho hình vuông ABCD có độ dài bằng cạnh a . Gọi P,Q ll là trung điểm của CD,DA . Tính overrightarrow{BQ}.overrightarrow{BP}Help me ! Tks
Đọc tiếp
1. Cho tam giác ABC có O là điểm thỏa mãn \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\) và OA=OB=OC. Gọi M ,N ll là trung điểm của BC,AC . Tính số đo của \(\left(\overrightarrow{AM,}\overrightarrow{BN}\right)\)
2. Cho hình vuông ABCD có độ dài bằng cạnh a . Gọi P,Q ll là trung điểm của CD,DA . Tính \(\overrightarrow{BQ}.\overrightarrow{BP}\)
Help me ! Tks
1.
Gọi G là trọng tâm tam giác
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{OG}=\overrightarrow{0}\)
\(\Leftrightarrow O\equiv G\)
\(\Rightarrow O\) là trọng tâm tam giác ABC
\(\Rightarrow\Delta ABC\) đều
Gọi độ dài các cạnh tam giác là a
\(\overrightarrow{BN}.\overrightarrow{AM}=\dfrac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=-\dfrac{1}{4}a^2-\dfrac{1}{8}a^2-\dfrac{1}{8}a^2+\dfrac{1}{2}a^2=0\)
Mặt khác \(\overrightarrow{BN}.\overrightarrow{AM}=BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)\)
\(\Rightarrow BN.AM.cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow cos\left(\overrightarrow{AM};\overrightarrow{BN}\right)=0\Rightarrow\left(\overrightarrow{AM};\overrightarrow{BN}\right)=90^o\)
Đúng 1
Bình luận (0)
\(BD=\dfrac{AB}{cos45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{BQ}.\overrightarrow{BP}=\dfrac{1}{4}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{4}BA.BC.cos90^o+\dfrac{1}{4}BA.BD.cos45^o+\dfrac{1}{4}BD.BC.cos45^o+\dfrac{1}{4}BD^2\)
\(=\dfrac{1}{4}a^2+\dfrac{1}{4}a^2+\dfrac{1}{2}a^2=a^2\)
Đúng 1
Bình luận (0)
cho tam giác ABC có AB=a, AC=2a, D là trung điẻm AC, M là điểm thoả mãn
\(\overrightarrow{BM}=\dfrac{1}{3}\overrightarrow{BC}\) . Tính \(\overrightarrow{BD}.\overrightarrow{AM}\)
Cho tam giác ABC vuông tại A có AB=a, AC=a\(\sqrt{3}\) và AM là trung tuyến. Tích vô hướng \(\overrightarrow{BA}.\overrightarrow{AM}\)
\(tanB=\dfrac{AC}{AB}=\sqrt{3}\Rightarrow B=60^0\)
\(\Rightarrow\widehat{BAM}=\widehat{B}=60^0\)
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)
\(\overrightarrow{BA}.\overrightarrow{AM}=-\overrightarrow{AB}.\overrightarrow{AM}=-AB.AM.cos\widehat{BAM}=-\dfrac{a^2}{2}\)
Đúng 1
Bình luận (0)
CHO tam giác ABC có I là trung điểm của trung tuyến AM và D là điểm thỏa hệ thức \(3\overrightarrow{AD}=\overrightarrow{AC}\)
A/ Biểu diễn vecto BD,BI theo AB,AC
b/ CHỨNG MINH BA ĐIỂM B,I, D THẲNG HÀNG


















