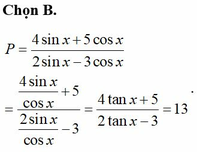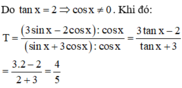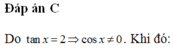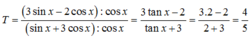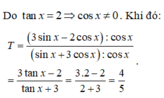a, \(sin^2x-4sinx+3=0\)

\(\Leftrightarrow\left(sinx-1\right)\left(sinx-3\right)=0\)

\(\Leftrightarrow sinx=1\)

\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)

b, \(2cos^2-cosx-1=0\)

\(\Leftrightarrow\left(cosx-1\right)\left(2cosx+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)

c, \(3sin^2x-2cosx+2=0\)

\(\Leftrightarrow3-3sin^2x+2cosx-5=0\)

\(\Leftrightarrow3cos^2x+2cosx-5=0\)

\(\Leftrightarrow\left(cosx-1\right)\left(3cosx+5\right)=0\)

\(\Leftrightarrow cosx=1\)

\(\Leftrightarrow x=k2\pi\)

tan x=-2

=>sin x/cosx=-2

=>sin x=-2*cosx

\(1+tan^2x=\dfrac{1}{cos^2x}\)

=>\(\dfrac{1}{cos^2x}=1+2=3\)

=>\(cos^2x=\dfrac{1}{3}\)

\(H=\dfrac{sin^3x+5\cdot cos^3x}{3\cdot sinx-2\cdot cosx}\)

\(=\dfrac{\left(-2\cdot cosx\right)^3+5\cdot cos^3x}{3\cdot\left(-2\right)\cdot cosx-2\cdot cosx}\)

\(=\dfrac{-8\cdot cos^3x+5\cdot cos^3x}{-6\cdot cos-2\cdot cosx}=\dfrac{-3\cdot cos^3x}{-8\cdot cosx}=\dfrac{3}{8}\cdot cos^2x\)

=3/8*1/3

=1/8

Đáp án C

Đáp án C

a/

\(\Leftrightarrow\frac{3}{\sqrt{13}}sinx-\frac{2}{\sqrt{13}}cosx=\frac{2}{\sqrt{13}}\)

Đặt \(cosa=\frac{3}{\sqrt{13}}\) với \(0< a< \pi\)

\(\Rightarrow sinx.cosa-cosx.sina=sina\)

\(\Leftrightarrow sin\left(x-a\right)=sina\)

\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=\pi-a+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

b/

\(\Leftrightarrow cosx.\frac{1}{\sqrt{17}}+sinx.\frac{4}{\sqrt{17}}=-\frac{1}{\sqrt{17}}\)

Đặt \(cosa=\frac{1}{\sqrt{17}}\) với \(0< a< \pi\)

\(\Rightarrow cosx.cosa+sinx.sina=-cosa\)

\(\Leftrightarrow cos\left(x-a\right)=cos\left(\pi-a\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-a=\pi-a+k2\pi\\x-a=a-\pi+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=2a-\pi+k2\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow\frac{\sqrt{3}}{\sqrt{19}}cosx+\frac{4}{\sqrt{19}}sinx=\frac{\sqrt{3}}{\sqrt{19}}\)

Đặt \(cosa=\frac{\sqrt{3}}{\sqrt{19}}\) với \(0< a< \pi\)

\(\Rightarrow cosx.cosa+sinx.sina=cosa\)

\(\Leftrightarrow cos\left(x-a\right)=cosa\)

\(\Rightarrow\left[{}\begin{matrix}x-a=a+k2\pi\\x-a=-a+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2a+k2\pi\\x=k2\pi\end{matrix}\right.\)

1) a) cos7x - √3 sin7x = -√2 (a = 1; b = -√3; c = -√2)

=> a^2 + b^2 =4 > c^2 = 2

Chia 2 vế pt (*) cho \(\sqrt{a^2+b^2}=2\) ta đc:

<=> 1/2cos7x - √3/2 sin7x = -√2/2

<=> sin(π/6)cos7x - cos(π/6)sin7x = sin(-π/4)

<=> sin(π/6 - 7x) = sin(-π/4)

<=> π/6 - 7x = -π/4 + k2π

hoặc (k∈Z)

π/6 - 7x = π + π/4 + k2π

<=> x = 5π/84 + k2π/7

hoặc (k∈Z)

x = -13π/84 + k2π/7

1) b) Ta có:

* 2π/5 < x < 6π/7

<=> 2π/5 < 5π/84 + k2π/7 < 6π/7

<=> 143π/420 < k2π/7 < 67π/84

<=> 143/120 < k < 67/24

=> k ϵ {2}

=> x = 53π/84

* 2π/5 < x < 6π/7

<=> 2π/5 < -13π/84 + k2π/7 < 6π/7

<=> 233/120 < k < 85/24

=> k ϵ {2; 3}

=> x = 5π/12 ; x = 59π/84

Vậy có tất cả 3 nghiệm thỏa mãn (2π/5;6π/7) là x = 53π/84; x = 5π/12 ; x = 59π/84.

\(tanx=\dfrac{sinx}{cosx}\)

\(\Rightarrow M=\dfrac{2sinx}{\dfrac{cosx}{\dfrac{4sinx}{cosx}}}-\dfrac{3cosx}{\dfrac{cosx}{\dfrac{7cosx}{cosx}}}\)

\(M=\dfrac{2tanx-3}{4tanx+7}\)

\(M=\dfrac{2.\left(-2\right)-3}{4.2+7}\)

\(M=\dfrac{1}{15}\)